المرجع الألكتروني للمعلوماتية
القرآن الكريم وعلومه
العقائد الإسلامية
الفقه وأصوله 
الرجال والحديث 
سيرة الرسول وآله 
علوم اللغة العربية 
الأدب العربي 
الأسرة والمجتمع 
الأخلاق والأدعية 
التاريخ 
الادارة والاقتصاد 
علم الفيزياء 
علم الكيمياء 
علم الأحياء 
الرياضيات 
الهندسة المدنية 
الزراعة 
الجغرافية 
القانون 
اللغة الأنكليزية 
الأخبار 
الإعلام 
مكتبة الصور 
أقلام بمختلف الألوان 
إضاءات
مفتاح
أجوبة الإستفتاءات الشرعية
وثائقيات
تاريخ الرياضيات
الرياضيات في الحضارات المختلفة
الرياضيات المتقطعة
الجبر
الهندسة
المعادلات التفاضلية و التكاملية
التحليل
علماء الرياضيات | Complete Residue System |
 809
 05:49 مساءً
date: 5-1-2020 |
Author : Guy, R. K. 
Book or Source : Covering Systems of Congruences." §F13 in Unsolved Problems in Number Theory, 2nd ed. New York: Springer-Verlag 
Page and Part : ...|
Read More
Date: 30-11-2020
804
Date: 7-10-2020
829
Date: 4-5-2020
923
|
A set of numbers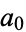 
, 
, ..., 
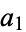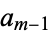(mod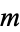 
) form a complete set of residues, also called a covering system, if they satisfy
 |
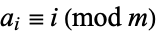for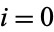 
, 1, ..., 
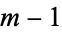. For example, a complete system of residues is formed by a base 
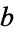and a modulus 
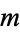if the residues 
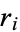in 
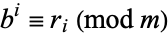for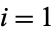 
, ..., 
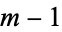run through the values 1, 2, ..., 
.
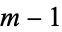REFERENCES:
Guy, R. K. "Covering Systems of Congruences." §F13 in Unsolved Problems in Number Theory, 2nd ed. New York: Springer-Verlag, pp. 251-253, 1994.
Nagell, T. "Residue Classes and Residue Systems." §20 in Introduction to Number Theory. New York: Wiley, pp. 69-71, 1951.
|
|
|
|
4 أسباب تجعلك تضيف الزنجبيل إلى طعامك.. تعرف عليها
|
|
|
|
|
|
|
أكبر محطة للطاقة الكهرومائية في بريطانيا تستعد للانطلاق
|
|
|
|
|
|
|
العتبة العباسية المقدسة تبحث مع العتبة الحسينية المقدسة التنسيق المشترك لإقامة حفل تخرج طلبة الجامعات
|
|
|
