


 تاريخ الرياضيات
تاريخ الرياضيات
 الرياضيات في الحضارات المختلفة
الرياضيات في الحضارات المختلفة 
 الرياضيات المتقطعة
الرياضيات المتقطعة
 الجبر
الجبر
 الهندسة
الهندسة 
 المعادلات التفاضلية و التكاملية
المعادلات التفاضلية و التكاملية 
 التحليل
التحليل
 علماء الرياضيات
علماء الرياضيات |
Read More
Date: 24-8-2020
Date: 16-2-2020
Date: 29-8-2020
|
A cyclotomic field 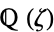 is obtained by adjoining a primitive root of unity
is obtained by adjoining a primitive root of unity 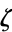 , say
, say 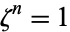 , to the rational numbers
, to the rational numbers 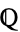 . Since
. Since 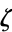 is primitive,
is primitive, 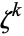 is also an
is also an 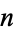 th root of unity and
th root of unity and 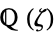 contains all of the
contains all of the 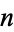 th roots of unity,
th roots of unity,
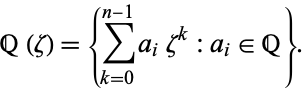 |
(1) |
For example, when 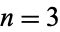 and
and 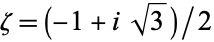 , the cyclotomic field is a quadratic field
, the cyclotomic field is a quadratic field
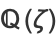 |
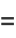 |
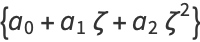 |
(2) |
 |
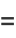 |
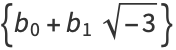 |
(3) |
 |
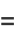 |
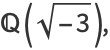 |
(4) |
where the coefficients 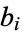 are contained in
are contained in 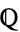 .
.
The Galois group of a cyclotomic field over the rationals is the multiplicative group of 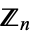 , the ring of integers (mod
, the ring of integers (mod 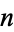 ). Hence, a cyclotomic field is a Abelian extension. Not all cyclotomic fields have unique factorization, for instance,
). Hence, a cyclotomic field is a Abelian extension. Not all cyclotomic fields have unique factorization, for instance, 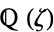 , where
, where 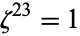 .
.
REFERENCES:
Fröhlich, A. and Taylor, M. Ch. 6 in Algebraic Number Theory. New York: Cambridge University Press, 1991.
Koch, H. "Cyclotomic Fields." §6.4 in Number Theory: Algebraic Numbers and Functions. Providence, RI: Amer. Math. Soc., pp. 180-184, 2000.
Weiss, E. Algebraic Number Theory. New York: Dover, 1998.



|
|
|
|
دخلت غرفة فنسيت ماذا تريد من داخلها.. خبير يفسر الحالة
|
|
|
|
|
|
|
ثورة طبية.. ابتكار أصغر جهاز لتنظيم ضربات القلب في العالم
|
|
|
|
|
|
|
سماحة السيد الصافي يؤكد ضرورة تعريف المجتمعات بأهمية مبادئ أهل البيت (عليهم السلام) في إيجاد حلول للمشاكل الاجتماعية
|
|
|