المرجع الألكتروني للمعلوماتية
القرآن الكريم وعلومه
العقائد الإسلامية
الفقه وأصوله 
الرجال والحديث 
سيرة الرسول وآله 
علوم اللغة العربية 
الأدب العربي 
الأسرة والمجتمع 
الأخلاق والأدعية 
التاريخ 
الادارة والاقتصاد 
علم الفيزياء 
علم الكيمياء 
علم الأحياء 
الرياضيات 
الهندسة المدنية 
الزراعة 
الجغرافية 
القانون 
اللغة الأنكليزية 
الأخبار 
الإعلام 
مكتبة الصور 
أقلام بمختلف الألوان 
إضاءات
مفتاح
أجوبة الإستفتاءات الشرعية
وثائقيات
تاريخ الرياضيات
الرياضيات في الحضارات المختلفة
الرياضيات المتقطعة
الجبر
الهندسة
المعادلات التفاضلية و التكاملية
التحليل
علماء الرياضيات | Havercosine |
 1813
 12:50 صباحاً
date: 10-10-2019 |
Author : المرجع الالكتروني للمعلوماتيه 
Book or Source : المرجع الالكتروني للمعلوماتيه 
Page and Part : ...|
Read More
Date:
1806
Date: 25-4-2019
2023
Date: 12-8-2018
1962
|
The havercosine, also called the haversed cosine, is a little-used trigonometric function defined by
 |
 |
 |
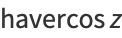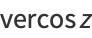(1) |
 |
 |
 |
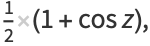(2) |
where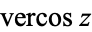 
is the vercosine and 
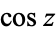is the cosine.
|
|
|
|
دخلت غرفة فنسيت ماذا تريد من داخلها.. خبير يفسر الحالة
|
|
|
|
|
|
|
ثورة طبية.. ابتكار أصغر جهاز لتنظيم ضربات القلب في العالم
|
|
|
|
|
|
|
قسم الشؤون الفكرية ينظم ندوة ثقافية بذكرى فاجعة هدم قبور أئمة البقيع (عليهم السلام)
|
|
|
