Riemann-Liouville Operator

The operator of fractional integration is defined as

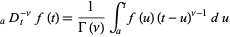for 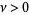 with 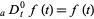 (Oldham and Spanier 1974, Miller and Ross 1993, Srivastava and Saxena 2001, Saxena 2002).

REFERENCES:

Miller, K. S. and Ross, B. An Introduction to the Fractional Calculus and Fractional Differential Equations. New York: Wiley, 1993.

Oldham, K. B. and Spanier, J. The Fractional Calculus: Integrations and Differentiations of Arbitrary Order. New York: Academic Press, 1974.

Saxena, R. K.; Mathai, A. M.; and Haubold, H. J. "On Fractional Kinetic Equations." 23 Jun 2002. http://arxiv.org/abs/math.CA/0206240.

Srivastava, H. M. and Saxena, R. K. "Operators of Fractional Integration and Their Applications." Appl. Math. and Comput. 118, 1-52, 2001.