


 تاريخ الرياضيات
تاريخ الرياضيات
 الرياضيات في الحضارات المختلفة
الرياضيات في الحضارات المختلفة 
 الرياضيات المتقطعة
الرياضيات المتقطعة
 الجبر
الجبر
 الهندسة
الهندسة 
 المعادلات التفاضلية و التكاملية
المعادلات التفاضلية و التكاملية 
 التحليل
التحليل
 علماء الرياضيات
علماء الرياضيات |
Read More
Date: 21-7-2019
Date: 21-8-2018
Date: 15-5-2019
|
The 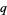 -binomial coefficient is a q-analog for the binomial coefficient, also called a Gaussian coefficient or a Gaussian polynomial. A
-binomial coefficient is a q-analog for the binomial coefficient, also called a Gaussian coefficient or a Gaussian polynomial. A 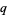 -binomial coefficient is given by
-binomial coefficient is given by
![[n; m]_q=((q)_n)/((q)_m(q)_(n-m))=product_(i=0)^(m-1)(1-q^(n-i))/(1-q^(i+1)),](http://mathworld.wolfram.com/images/equations/q-BinomialCoefficient/NumberedEquation1.gif) |
(1) |
where
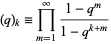 |
(2) |
is a q-series (Koepf 1998, p. 26). For 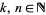 ,
,
![[n; k]_q=([n]_q!)/([k]_q![n-k]_q!),](http://mathworld.wolfram.com/images/equations/q-BinomialCoefficient/NumberedEquation3.gif) |
(3) |
where ![[n]_q!](http://mathworld.wolfram.com/images/equations/q-BinomialCoefficient/Inline4.gif) is a q-factorial (Koepf 1998, p. 30). The
is a q-factorial (Koepf 1998, p. 30). The 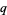 -binomial coefficient can also be defined in terms of the q-brackets
-binomial coefficient can also be defined in terms of the q-brackets ![[k]_q](http://mathworld.wolfram.com/images/equations/q-BinomialCoefficient/Inline6.gif) by
by
![[n; k]_q={product_(i=1)^(k)([n-i+1]_q)/([i]_q) for 0<=k<=n; 0 otherwise.](http://mathworld.wolfram.com/images/equations/q-BinomialCoefficient/NumberedEquation4.gif) |
(4) |
The 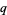 -binomial is implemented in the Wolfram Language as QBinomial[n, m, q].
-binomial is implemented in the Wolfram Language as QBinomial[n, m, q].
For 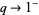 , the
, the 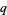 -binomial coefficients turn into the usual binomial coefficient.
-binomial coefficients turn into the usual binomial coefficient.
The special case
![[n]_q=[n; 1]_q=(1-q^n)/(1-q)](http://mathworld.wolfram.com/images/equations/q-BinomialCoefficient/NumberedEquation5.gif) |
(5) |
is sometimes known as the q-bracket.
The 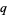 -binomial coefficient satisfies the recurrence equation
-binomial coefficient satisfies the recurrence equation
![[n+1; k]_q=q^k[n; k]_q+[n; k-1]_q,](http://mathworld.wolfram.com/images/equations/q-BinomialCoefficient/NumberedEquation6.gif) |
(6) |
for all 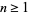 and
and 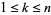 , so every
, so every 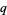 -binomial coefficient is a polynomial in
-binomial coefficient is a polynomial in 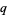 . The first few
. The first few 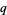 -binomial coefficients are
-binomial coefficients are
![[2; 1]_q](http://mathworld.wolfram.com/images/equations/q-BinomialCoefficient/Inline16.gif) |
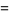 |
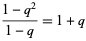 |
(7) |
![[3; 1]_q](http://mathworld.wolfram.com/images/equations/q-BinomialCoefficient/Inline19.gif) |
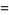 |
![[3; 2]_q=(1-q^3)/(1-q)=1+q+q^2](http://mathworld.wolfram.com/images/equations/q-BinomialCoefficient/Inline21.gif) |
(8) |
![[4; 1]_q](http://mathworld.wolfram.com/images/equations/q-BinomialCoefficient/Inline22.gif) |
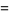 |
![[4; 3]_q=(1-q^4)/(1-q)=1+q+q^2+q^3](http://mathworld.wolfram.com/images/equations/q-BinomialCoefficient/Inline24.gif) |
(9) |
![[4; 2]_q](http://mathworld.wolfram.com/images/equations/q-BinomialCoefficient/Inline25.gif) |
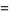 |
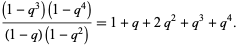 |
(10) |
From the definition, it follows that
![[n; 1]_q=[n; n-1]_q=sum_(i=0)^(n-1)q^i.](http://mathworld.wolfram.com/images/equations/q-BinomialCoefficient/NumberedEquation7.gif) |
(11) |
Additional identities include
![([n+1; k+1]_q)/([n; k+1]_q)](http://mathworld.wolfram.com/images/equations/q-BinomialCoefficient/Inline28.gif) |
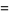 |
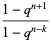 |
(12) |
![([n+1; k+1]_q)/([n+1; k]_q)](http://mathworld.wolfram.com/images/equations/q-BinomialCoefficient/Inline31.gif) |
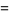 |
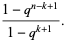 |
(13) |
The 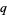 -binomial coefficient
-binomial coefficient ![[n; m]_q](http://mathworld.wolfram.com/images/equations/q-BinomialCoefficient/Inline35.gif) can be constructed by building all
can be constructed by building all 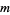 -subsets of
-subsets of 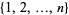 , summing the elements of each subset, and taking the sum
, summing the elements of each subset, and taking the sum
![[n; m]_q=sum_(i)q^(s_i-m(m+1)/2)](http://mathworld.wolfram.com/images/equations/q-BinomialCoefficient/NumberedEquation8.gif) |
(14) |
over all subset-sums 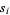 (Kac and Cheung 2001, p. 19).
(Kac and Cheung 2001, p. 19).
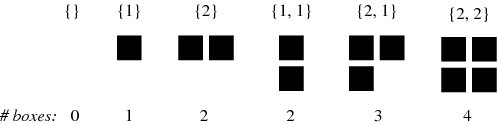
The 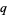 -binomial coefficient
-binomial coefficient ![[m+n; m]_q](http://mathworld.wolfram.com/images/equations/q-BinomialCoefficient/Inline40.gif) can also be interpreted as a polynomial in
can also be interpreted as a polynomial in 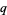 whose coefficient
whose coefficient 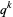 counts the number of distinct partitions of
counts the number of distinct partitions of 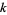 elements which fit inside an
elements which fit inside an 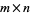 rectangle. For example, the partitions of 1, 2, 3, and 4 are given in the following table.
rectangle. For example, the partitions of 1, 2, 3, and 4 are given in the following table.
 |
partitions |
| 0 |  |
| 1 | 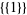 |
| 2 | 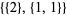 |
| 3 | 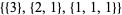 |
| 4 | 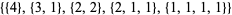 |
Of these, 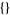 ,
, 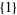 ,
, 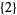 ,
, 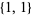 ,
, 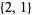 , and
, and 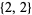 fit inside a
fit inside a 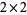 box. The counts of these having 0, 1, 2, 3, and 4 elements are 1, 1, 2, 1, and 1, so the (4, 2)-binomial coefficient is given by
box. The counts of these having 0, 1, 2, 3, and 4 elements are 1, 1, 2, 1, and 1, so the (4, 2)-binomial coefficient is given by
![[4; 2]_q=1+q+2q^2+q^3+q^4,](http://mathworld.wolfram.com/images/equations/q-BinomialCoefficient/NumberedEquation9.gif) |
(15) |
as above.
REFERENCES:
Gasper, G. and Rahman, M. Basic Hypergeometric Series. Cambridge, England: Cambridge University Press, 1990.
Kac, V. Cheung, P. Quantum Calculus. New York:Springer-Verlag, 2001.
Koekoek, R. and Swarttouw, R. F. "The q-Gamma Function and the q-Binomial Coefficient." §0.3 in The Askey-Scheme of Hypergeometric Orthogonal Polynomials and its q-Analogue. Delft, Netherlands: Technische Universiteit Delft, Faculty of Technical Mathematics and Informatics Report 98-17, pp. 10-11, 1998.
Koepf, W. Hypergeometric Summation: An Algorithmic Approach to Summation and Special Function Identities. Braunschweig, Germany: Vieweg, p. 26, 1998.a



|
|
|
|
دخلت غرفة فنسيت ماذا تريد من داخلها.. خبير يفسر الحالة
|
|
|
|
|
|
|
ثورة طبية.. ابتكار أصغر جهاز لتنظيم ضربات القلب في العالم
|
|
|
|
|
|
|
العتبة العباسية المقدسة تقدم دعوة لجامعة سومر للمشاركة في حفل التخرج المركزي الخامس
|
|
|