


 تاريخ الرياضيات
تاريخ الرياضيات
 الرياضيات في الحضارات المختلفة
الرياضيات في الحضارات المختلفة 
 الرياضيات المتقطعة
الرياضيات المتقطعة
 الجبر
الجبر
 الهندسة
الهندسة 
 المعادلات التفاضلية و التكاملية
المعادلات التفاضلية و التكاملية 
 التحليل
التحليل
 علماء الرياضيات
علماء الرياضيات |
Read More
Date: 17-9-2018
Date: 18-7-2019
Date: 23-9-2019
|
The Lerch transcendent is generalization of the Hurwitz zeta function and polylogarithm function. Many sums of reciprocal powers can be expressed in terms of it. It is classically defined by
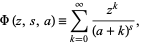 |
(1) |
for 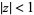 and
and 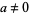 ,
, 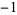 , .... It is implemented in this form as HurwitzLerchPhi[z, s, a] in the Wolfram Language.
, .... It is implemented in this form as HurwitzLerchPhi[z, s, a] in the Wolfram Language.
The slightly different form
![Phi^*(z,s,a)=sum_(k=0)^infty(z^k)/([(a+k)^2]^(s/2))](http://mathworld.wolfram.com/images/equations/LerchTranscendent/NumberedEquation2.gif) |
(2) |
sometimes also denoted 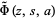 , for
, for 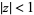 (or
(or 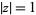 and
and ![R[s]>1](http://mathworld.wolfram.com/images/equations/LerchTranscendent/Inline7.gif) ) and
) and 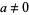 ,
, 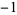 ,
, 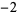 , ..., is implemented in the Wolfram Language as LerchPhi[z, s, a]. Note that the two are identical only for
, ..., is implemented in the Wolfram Language as LerchPhi[z, s, a]. Note that the two are identical only for ![R[a]>0](http://mathworld.wolfram.com/images/equations/LerchTranscendent/Inline11.gif) .
.
A series formula for 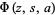 valid on a larger domain in the complex
valid on a larger domain in the complex 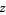 -plane is given by
-plane is given by
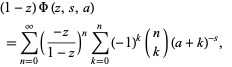 |
(3) |
which holds for all complex 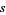 and complex
and complex 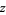 with
with ![R[z]<1/2](http://mathworld.wolfram.com/images/equations/LerchTranscendent/Inline16.gif) (Guillera and Sondow 2005).
(Guillera and Sondow 2005).
The Lerch transcendent can be used to express the Dirichlet beta function
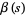 |
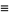 |
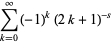 |
(4) |
 |
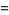 |
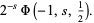 |
(5) |
A special case is given by
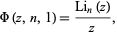 |
(6) |
(Guillera and Sondow 2005), where 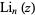 is the polylogarithm.
is the polylogarithm.
Special cases giving simple constants include
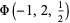 |
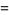 |
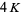 |
(7) |
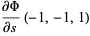 |
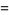 |
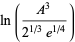 |
(8) |
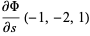 |
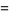 |
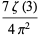 |
(9) |
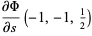 |
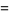 |
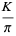 |
(10) |
where 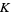 is Catalan's constant,
is Catalan's constant, 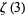 is Apéry's constant, and
is Apéry's constant, and 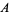 is the Glaisher-Kinkelin constant (Guillera and Sondow 2005).
is the Glaisher-Kinkelin constant (Guillera and Sondow 2005).
It gives the integrals of the Fermi-Dirac distribution
 |
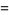 |
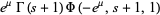 |
(11) |
 |
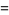 |
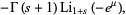 |
(12) |
where 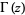 is the gamma function and
is the gamma function and 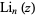 is the polylogarithm and Bose-Einstein distribution
is the polylogarithm and Bose-Einstein distribution
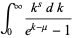 |
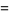 |
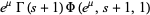 |
(13) |
 |
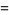 |
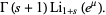 |
(14) |
Double integrals involving the Lerch transcendent include
![int_0^1int_0^1(x^(u-1)y^(v-1))/(1-xyz)[-ln(xy)]^sdxdy
=Gamma(s+1)(Phi(z,s+1,v)-Phi(z,s+1,u))/(u-v)
int_0^1int_0^1((xy)^(u-1))/(1-xyz)[-ln(xy)]^sdxdy
=Gamma(s)Phi(z,s+2,u),](http://mathworld.wolfram.com/images/equations/LerchTranscendent/NumberedEquation5.gif) |
(15) |
where 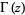 is the gamma function. These formulas lead to a variety of beautiful special cases of unit square integrals (Guillera and Sondow 2005).
is the gamma function. These formulas lead to a variety of beautiful special cases of unit square integrals (Guillera and Sondow 2005).
It also can be used to evaluate Dirichlet L-series.
REFERENCES:
Erdélyi, A.; Magnus, W.; Oberhettinger, F.; and Tricomi, F. G. "The Function 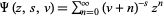 ." §1.11 in Higher Transcendental Functions, Vol. 1. New York: Krieger, pp. 27-31, 1981.
." §1.11 in Higher Transcendental Functions, Vol. 1. New York: Krieger, pp. 27-31, 1981.
Gradshteyn, I. S. and Ryzhik, I. M. "The Lerch Function 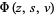 ." §9.55 in Tables of Integrals, Series, and Products, 6th ed. San Diego, CA: Academic Press, p. 1029, 2000.
." §9.55 in Tables of Integrals, Series, and Products, 6th ed. San Diego, CA: Academic Press, p. 1029, 2000.
Guillera, J. and Sondow, J. "Double Integrals and Infinite Products for Some Classical Constants Via Analytic Continuations of Lerch's Transcendent." 16 June 2005 http://arxiv.org/abs/math.NT/0506319.



|
|
|
|
4 أسباب تجعلك تضيف الزنجبيل إلى طعامك.. تعرف عليها
|
|
|
|
|
|
|
أكبر محطة للطاقة الكهرومائية في بريطانيا تستعد للانطلاق
|
|
|
|
|
|
|
العتبة العباسية المقدسة تبحث مع العتبة الحسينية المقدسة التنسيق المشترك لإقامة حفل تخرج طلبة الجامعات
|
|
|