
Spherical Harmonic
 المؤلف:
Abbott, P
المؤلف:
Abbott, P
 المصدر:
"2. Schrödinger Equation." Lecture Notes for Computational Physics 2. http://physics.uwa.edu.au/pub/Computational/CP2/2.Schroedinger.nb.
المصدر:
"2. Schrödinger Equation." Lecture Notes for Computational Physics 2. http://physics.uwa.edu.au/pub/Computational/CP2/2.Schroedinger.nb.
 الجزء والصفحة:
...
الجزء والصفحة:
...
 6-8-2019
6-8-2019
 3866
3866
Spherical Harmonic
The spherical harmonics 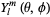 are the angular portion of the solution to Laplace's equation in spherical coordinates where azimuthal symmetry is not present. Some care must be taken in identifying the notational convention being used. In this entry,
are the angular portion of the solution to Laplace's equation in spherical coordinates where azimuthal symmetry is not present. Some care must be taken in identifying the notational convention being used. In this entry, 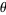 is taken as the polar (colatitudinal) coordinate with
is taken as the polar (colatitudinal) coordinate with ![theta in [0,pi]](http://mathworld.wolfram.com/images/equations/SphericalHarmonic/Inline3.gif) , and
, and 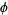 as the azimuthal (longitudinal) coordinate with
as the azimuthal (longitudinal) coordinate with 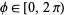 . This is the convention normally used in physics, as described by Arfken (1985) and the Wolfram Language (in mathematical literature,
. This is the convention normally used in physics, as described by Arfken (1985) and the Wolfram Language (in mathematical literature, 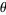 usually denotes the longitudinal coordinate and
usually denotes the longitudinal coordinate and 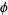 the colatitudinal coordinate). Spherical harmonics are implemented in the Wolfram Language as SphericalHarmonicY[l, m, theta, phi].
the colatitudinal coordinate). Spherical harmonics are implemented in the Wolfram Language as SphericalHarmonicY[l, m, theta, phi].
Spherical harmonics satisfy the spherical harmonic differential equation, which is given by the angular part of Laplace's equation in spherical coordinates. Writing 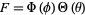 in this equation gives
in this equation gives
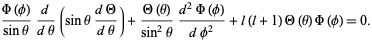 |
(1)
|
Multiplying by 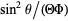 gives
gives
![[(sintheta)/(Theta(theta))d/(dtheta)(sintheta(dTheta)/(dtheta))+l(l+1)sin^2theta]+1/(Phi(phi))(d^2Phi(phi))/(dphi^2)=0.](http://mathworld.wolfram.com/images/equations/SphericalHarmonic/NumberedEquation2.gif) |
(2)
|
Using separation of variables by equating the 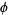 -dependent portion to a constant gives
-dependent portion to a constant gives
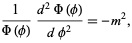 |
(3)
|
which has solutions
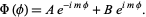 |
(4)
|
Plugging in (3) into (2) gives the equation for the 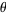 -dependent portion, whose solution is
-dependent portion, whose solution is
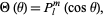 |
(5)
|
where 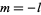 ,
, 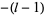 , ..., 0, ...,
, ..., 0, ..., 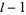 ,
, 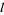 and
and 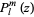 is an associated Legendre polynomial. The spherical harmonics are then defined by combining
is an associated Legendre polynomial. The spherical harmonics are then defined by combining 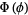 and
and 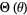 ,
,
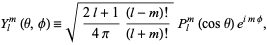 |
(6)
|
where the normalization is chosen such that
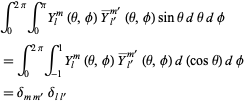 |
(7)
|
(Arfken 1985, p. 681). Here, 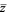 denotes the complex conjugate and
denotes the complex conjugate and 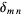 is the Kronecker delta. Sometimes (e.g., Arfken 1985), the Condon-Shortley phase
is the Kronecker delta. Sometimes (e.g., Arfken 1985), the Condon-Shortley phase 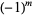 is prepended to the definition of the spherical harmonics.
is prepended to the definition of the spherical harmonics.
The spherical harmonics are sometimes separated into their real and imaginary parts,
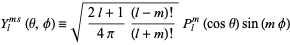 |
(8)
|
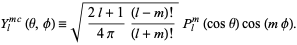 |
(9)
|
The spherical harmonics obey
where 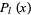 is a Legendre polynomial.
is a Legendre polynomial.
Integrals of the spherical harmonics are given by
 |
(13)
|
where 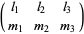 is a Wigner 3j-symbol (which is related to the Clebsch-Gordan coefficients). Special cases include
is a Wigner 3j-symbol (which is related to the Clebsch-Gordan coefficients). Special cases include
(Arfken 1985, p. 700).
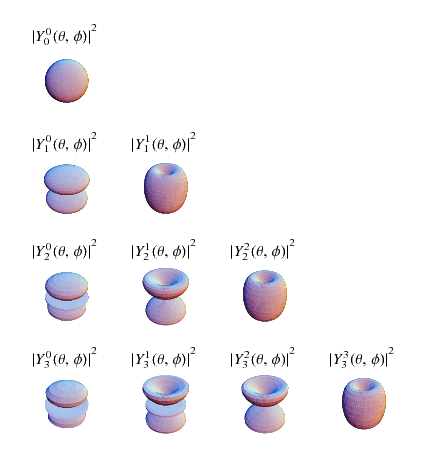
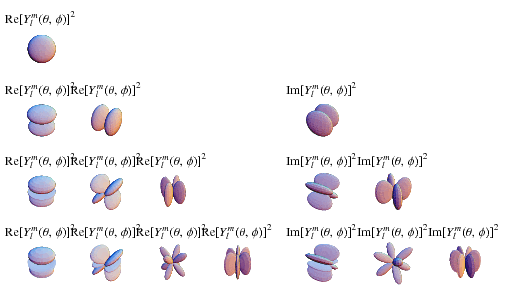
The above illustrations show 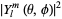 (top),
(top), ![R[Y_l^m(theta,phi)]^2](http://mathworld.wolfram.com/images/equations/SphericalHarmonic/Inline46.gif) (bottom left), and
(bottom left), and ![I[Y_l^m(theta,phi)]^2](http://mathworld.wolfram.com/images/equations/SphericalHarmonic/Inline47.gif) (bottom right). The first few spherical harmonics are
(bottom right). The first few spherical harmonics are
Written in terms of Cartesian coordinates,
so
The zonal harmonics are defined to be those of the form
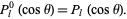 |
(43)
|
The tesseral harmonics are those of the form
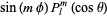 |
(44)
|
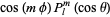 |
(45)
|
for 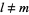 . The sectorial harmonics are of the form
. The sectorial harmonics are of the form
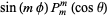 |
(46)
|
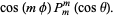 |
(47)
|
REFERENCES:
Abbott, P. "2. Schrödinger Equation." Lecture Notes for Computational Physics 2. http://physics.uwa.edu.au/pub/Computational/CP2/2.Schroedinger.nb.
Arfken, G. "Spherical Harmonics" and "Integrals of the Products of Three Spherical Harmonics." §12.6 and 12.9 in Mathematical Methods for Physicists, 3rd ed. Orlando, FL: Academic Press, pp. 680-685 and 698-700, 1985.
Byerly, W. E. "Spherical Harmonics." Ch. 6 in An Elementary Treatise on Fourier's Series, and Spherical, Cylindrical, and Ellipsoidal Harmonics, with Applications to Problems in Mathematical Physics. New York: Dover, pp. 195-218, 1959.
Ferrers, N. M. An Elementary Treatise on Spherical Harmonics and Subjects Connected with Them. London: Macmillan, 1877.
Groemer, H. Geometric Applications of Fourier Series and Spherical Harmonics. New York: Cambridge University Press, 1996.
Hobson, E. W. The Theory of Spherical and Ellipsoidal Harmonics. New York: Chelsea, 1955.
Kalf, H. "On the Expansion of a Function in Terms of Spherical Harmonics in Arbitrary Dimensions." Bull. Belg. Math. Soc. Simon Stevin 2, 361-380, 1995.
MacRobert, T. M. and Sneddon, I. N. Spherical Harmonics: An Elementary Treatise on Harmonic Functions, with Applications, 3rd ed. rev. Oxford, England: Pergamon Press, 1967.
Normand, J. M. A Lie Group: Rotations in Quantum Mechanics. Amsterdam, Netherlands: North-Holland, 1980.
Press, W. H.; Flannery, B. P.; Teukolsky, S. A.; and Vetterling, W. T. "Spherical Harmonics." §6.8 in Numerical Recipes in FORTRAN: The Art of Scientific Computing, 2nd ed. Cambridge, England: Cambridge University Press, pp. 246-248, 1992.
Sansone, G. "Harmonic Polynomials and Spherical Harmonics," "Integral Properties of Spherical Harmonics and the Addition Theorem for Legendre Polynomials," and "Completeness of Spherical Harmonics with Respect to Square Integrable Functions." §3.18-3.20 in Orthogonal Functions, rev. English ed. New York: Dover, pp. 253-272, 1991.
Sternberg, W. and Smith, T. L. The Theory of Potential and Spherical Harmonics, 2nd ed. Toronto: University of Toronto Press, 1946.
Wang, J.; Abbott, P.; and Williams, J. "Visualizing Atomic Orbitals." http://physics.uwa.edu.au/pub/Orbitals.
Weisstein, E. W. "Books about Spherical Harmonics." http://www.ericweisstein.com/encyclopedias/books/SphericalHarmonics.html.
Whittaker, E. T. and Watson, G. N. "Solution of Laplace's Equation Involving Legendre Functions" and "The Solution of Laplace's Equation which Satisfies Assigned Boundary Conditions at the Surface of a Sphere." §18.31 and 18.4 in A Course in Modern Analysis, 4th ed. Cambridge, England: Cambridge University Press, pp. 391-395, 1990.
Zwillinger, D. Handbook of Differential Equations, 3rd ed. Boston, MA: Academic Press, p. 129, 1997.
 الاكثر قراءة في التفاضل و التكامل
الاكثر قراءة في التفاضل و التكامل
 اخر الاخبار
اخر الاخبار
اخبار العتبة العباسية المقدسة


