Gegenbauer Polynomial

The Gegenbauer polynomials 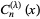 are solutions to the Gegenbauer differential equation for integer 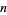. They are generalizations of the associated Legendre polynomials to 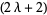-D space, and are proportional to (or, depending on the normalization, equal to) the ultraspherical polynomials .

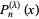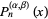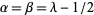Following Szegö, in this work, Gegenbauer polynomials are given in terms of the Jacobi polynomials  with  by

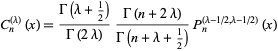(1)

(Szegö 1975, p. 80), thus making them equivalent to the Gegenbauer polynomials implemented in the Wolfram Language as GegenbauerC[n, lambda, x]. These polynomials are also given by the generating function

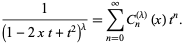(2)

The first few Gegenbauer polynomials are

			(3)
			(4)
			(5)
			(6)

In terms of the hypergeometric functions,

			(7)
			(8)
			(9)

They are normalized by

(10)

for .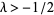

Derivative identities include

			(11)
			(12)
			(13)
			(14)
			(15)
			(16)
			(17)
			(18)

(Szegö 1975, pp. 80-83).

A recurrence relation is

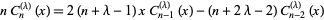(19)

for 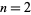, 3, ....

Special double- formulas also exist

			(20)
			(21)
			(22)
			(23)

Koschmieder (1920) gives representations in terms of elliptic functions for 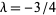 and .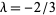

REFERENCES:

Abramowitz, M. and Stegun, I. A. (Eds.). "Orthogonal Polynomials." Ch. 22 in Handbook of Mathematical Functions with Formulas, Graphs, and Mathematical Tables, 9th printing. New York: Dover, pp. 771-802, 1972.

Arfken, G. Mathematical Methods for Physicists, 3rd ed. Orlando, FL: Academic Press, p. 643, 1985.

Erdélyi, A.; Magnus, W.; Oberhettinger, F.; and Tricomi, F. G. Higher Transcendental Functions, Vol. 2. New York: Krieger, p. 175, 1981.

Infeld, L. and Hull, T. E. "The Factorization Method." Rev. Mod. Phys. 23, 21-68, 1951.

Iyanaga, S. and Kawada, Y. (Eds.). "Gegenbauer Polynomials (Gegenbauer Functions)." Appendix A, Table 20.I in Encyclopedic Dictionary of Mathematics. Cambridge, MA: MIT Press, pp. 1477-1478, 1980.

Koekoek, R. and Swarttouw, R. F. "Gegenbauer / Ultraspherical." §1.8.1 in The Askey-Scheme of Hypergeometric Orthogonal Polynomials and its 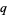-Analogue. Delft, Netherlands: Technische Universiteit Delft, Faculty of Technical Mathematics and Informatics Report 98-17, pp. 40-41, 1998.

Koschmieder, L. "Über besondere Jacobische Polynome." Math. Zeitschrift 8, 123-137, 1920.

Morse, P. M. and Feshbach, H. Methods of Theoretical Physics, Part I. New York: McGraw-Hill, pp. 547-549 and 600-604, 1953.

Roman, S. "A Particular Delta Series and the Gegenbauer Polynomials." §6.3 in The Umbral Calculus. New York: Academic Press, pp. 166-174, 1984.

Szegö, G. Orthogonal Polynomials, 4th ed. Providence, RI: Amer. Math. Soc., 1975.

Zwillinger, D. Handbook of Differential Equations, 3rd ed. Boston, MA: Academic Press, pp. 122-123, 1997.