


 تاريخ الرياضيات
تاريخ الرياضيات
 الرياضيات في الحضارات المختلفة
الرياضيات في الحضارات المختلفة 
 الرياضيات المتقطعة
الرياضيات المتقطعة
 الجبر
الجبر
 الهندسة
الهندسة 
 المعادلات التفاضلية و التكاملية
المعادلات التفاضلية و التكاملية 
 التحليل
التحليل
 علماء الرياضيات
علماء الرياضيات |
Read More
Date: 15-5-2018
Date: 25-5-2019
Date: 12-10-2019
|
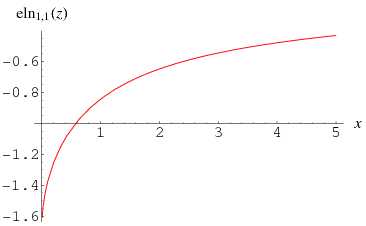
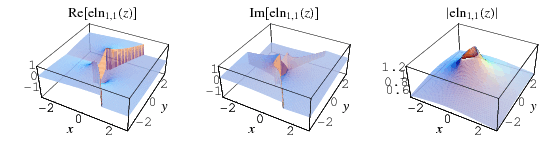
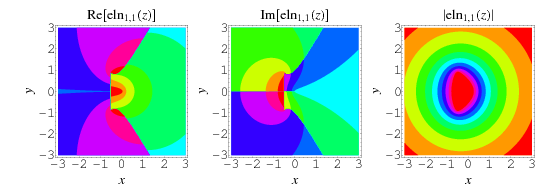
The elliptic logarithm is generalization of integrals of the form
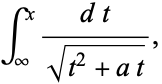 |
for 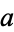 real, which can be expressed in terms of logarithmic and inverse trigonometric functions, to
real, which can be expressed in terms of logarithmic and inverse trigonometric functions, to
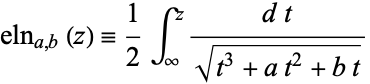 |
for 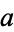 and
and 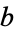 real. This integral can be done analytically, but has a complicated form involving incomplete elliptic integrals of the first kind with complex parameters. The plots above show the special case
real. This integral can be done analytically, but has a complicated form involving incomplete elliptic integrals of the first kind with complex parameters. The plots above show the special case 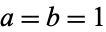 .
.
The elliptic logarithm is implemented in the Wolfram Language as EllipticLog[ x, y
x, y ,
,  a, b
a, b ], where
], where 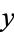 is an unfortunate and superfluous parameter that must be set to either
is an unfortunate and superfluous parameter that must be set to either 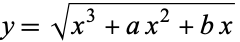 or
or 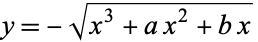 and which multiplies the above integral by a factor of
and which multiplies the above integral by a factor of 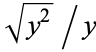 .
.
The inverse of the elliptic logarithm is the elliptic exponential function.
REFERENCES:
Wolfram, S. The Mathematica Book, 5th ed. Champaign, IL: Wolfram Media, p. 788, 2003.



|
|
|
|
التوتر والسرطان.. علماء يحذرون من "صلة خطيرة"
|
|
|
|
|
|
|
مرآة السيارة: مدى دقة عكسها للصورة الصحيحة
|
|
|
|
|
|
|
نحو شراكة وطنية متكاملة.. الأمين العام للعتبة الحسينية يبحث مع وكيل وزارة الخارجية آفاق التعاون المؤسسي
|
|
|