

تاريخ الرياضيات

الاعداد و نظريتها

تاريخ التحليل

تار يخ الجبر

الهندسة و التبلوجي


الرياضيات في الحضارات المختلفة

العربية

اليونانية

البابلية

الصينية

المايا

المصرية

الهندية


الرياضيات المتقطعة

المنطق

اسس الرياضيات

فلسفة الرياضيات

مواضيع عامة في المنطق


الجبر

الجبر الخطي

الجبر المجرد

الجبر البولياني

مواضيع عامة في الجبر

الضبابية

نظرية المجموعات

نظرية الزمر

نظرية الحلقات والحقول

نظرية الاعداد

نظرية الفئات

حساب المتجهات

المتتاليات-المتسلسلات

المصفوفات و نظريتها

المثلثات


الهندسة

الهندسة المستوية

الهندسة غير المستوية

مواضيع عامة في الهندسة

التفاضل و التكامل


المعادلات التفاضلية و التكاملية

معادلات تفاضلية

معادلات تكاملية

مواضيع عامة في المعادلات


التحليل

التحليل العددي

التحليل العقدي

التحليل الدالي

مواضيع عامة في التحليل

التحليل الحقيقي

التبلوجيا

نظرية الالعاب

الاحتمالات و الاحصاء

نظرية التحكم

بحوث العمليات

نظرية الكم

الشفرات

الرياضيات التطبيقية

نظريات ومبرهنات


علماء الرياضيات

500AD

500-1499

1000to1499

1500to1599

1600to1649

1650to1699

1700to1749

1750to1779

1780to1799

1800to1819

1820to1829

1830to1839

1840to1849

1850to1859

1860to1864

1865to1869

1870to1874

1875to1879

1880to1884

1885to1889

1890to1894

1895to1899

1900to1904

1905to1909

1910to1914

1915to1919

1920to1924

1925to1929

1930to1939

1940to the present

علماء الرياضيات

الرياضيات في العلوم الاخرى

بحوث و اطاريح جامعية

هل تعلم

طرائق التدريس

الرياضيات العامة

نظرية البيان
Jack Polynomial
المؤلف:
Dumitriu, I.; Edelman, A.; and Shuman, G.
المصدر:
"MOPS: Multivariate Orthogonal Polynomials (Symbolically)." Preprint. March 26
الجزء والصفحة:
...
28-7-2019
1559
Jack Polynomial
The Jack polynomials are a family of multivariate orthogonal polynomials dependent on a positive parameter 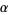 . Orthogonality of the Jack polynomials is proved in Macdonald (1995, p. 383). The Jack polynomials have a rich history, and special cases of
. Orthogonality of the Jack polynomials is proved in Macdonald (1995, p. 383). The Jack polynomials have a rich history, and special cases of 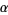 have been studied more extensively than others (Dumitriu et al. 2004). The following table summarizes some of these special cases.
have been studied more extensively than others (Dumitriu et al. 2004). The following table summarizes some of these special cases.
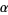 |
special polynomial |
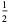 |
quaternion zonal polynomial |
| 1 | Schur polynomial |
| 2 | zonal polynomial |
Jack (1969-1970) originally defined the polynomials that eventually became associated with his name while attempting to evaluate an integral connected with the noncentral Wishart distribution (James 1960, Hua 1963, Dumitriu et al. 2004). Jack noted that the case 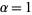 were the Schur polynomials, and conjectured that
were the Schur polynomials, and conjectured that 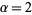 were the zonal polynomials. The question of finding a combinatorial interpretation for the polynomials was raised by Foulkes (1974), and subsequently answered by Knop and Sahi (1997). Later authors then generalized many known properties of the Schur and zonal polynomials to Jack polynomials (Stanley 1989, Macdonald 1995). Jack polynomials are especially useful in the theory of random matrices (Dumitriu et al. 2004).
were the zonal polynomials. The question of finding a combinatorial interpretation for the polynomials was raised by Foulkes (1974), and subsequently answered by Knop and Sahi (1997). Later authors then generalized many known properties of the Schur and zonal polynomials to Jack polynomials (Stanley 1989, Macdonald 1995). Jack polynomials are especially useful in the theory of random matrices (Dumitriu et al. 2004).
The Jack polynomials generalize the monomial scalar functions 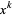 , which is orthogonal over the unit circle
, which is orthogonal over the unit circle 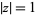 in the complex plane with weight function unity
in the complex plane with weight function unity 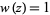 . The interval for the
. The interval for the 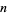 -multivariate Jack polynomials
-multivariate Jack polynomials 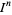 can therefore be thought of as an
can therefore be thought of as an 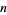 -dimensional torus (Dumitriu et al. 2004).
-dimensional torus (Dumitriu et al. 2004).
The Jack polynomials have several equivalent definitions (up to certain normalization constraints), and three common normalizations ("C," "J," and "P"). The "J" normalization makes the coefficient of the lowest-order monomial ![[1^n]](http://mathworld.wolfram.com/images/equations/JackPolynomial/Inline13.gif) equal to exactly
equal to exactly 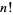 , while the "P" normalization is monic.
, while the "P" normalization is monic.
Letting ![m_([i_1,...,i_l])](http://mathworld.wolfram.com/images/equations/JackPolynomial/Inline15.gif) denote
denote 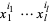 , the first few Jack "J" polynomials are given by
, the first few Jack "J" polynomials are given by
![J_([1])^alpha](http://mathworld.wolfram.com/images/equations/JackPolynomial/Inline17.gif) |
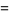 |
![m_([i])](http://mathworld.wolfram.com/images/equations/JackPolynomial/Inline19.gif) |
(1) |
![J_([2])^alpha](http://mathworld.wolfram.com/images/equations/JackPolynomial/Inline20.gif) |
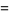 |
![(1+alpha)m_([2])+2m_([1,1])](http://mathworld.wolfram.com/images/equations/JackPolynomial/Inline22.gif) |
(2) |
![J_([1,1])^alpha](http://mathworld.wolfram.com/images/equations/JackPolynomial/Inline23.gif) |
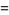 |
![2m_([1,1])](http://mathworld.wolfram.com/images/equations/JackPolynomial/Inline25.gif) |
(3) |
![J_([3])^alpha](http://mathworld.wolfram.com/images/equations/JackPolynomial/Inline26.gif) |
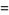 |
![(1+alpha)(2+alpha)m_([3])+3(1+alpha)m_([2,1])+6m_([1,1,1])](http://mathworld.wolfram.com/images/equations/JackPolynomial/Inline28.gif) |
(4) |
![J_([2,1])^alpha](http://mathworld.wolfram.com/images/equations/JackPolynomial/Inline29.gif) |
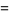 |
![(2+alpha)m_([2,1])+6m_([1,1,1])](http://mathworld.wolfram.com/images/equations/JackPolynomial/Inline31.gif) |
(5) |
![J_([1,1,1])^alpha](http://mathworld.wolfram.com/images/equations/JackPolynomial/Inline32.gif) |
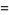 |
![6m_([1,1,1])](http://mathworld.wolfram.com/images/equations/JackPolynomial/Inline34.gif) |
(6) |
(Dumitriu et al. 2004).
Let ![lambda=[a_1,a_2,...,a_(l(lambda))]](http://mathworld.wolfram.com/images/equations/JackPolynomial/Inline35.gif) be a partition, then the Jack polynomials
be a partition, then the Jack polynomials 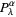 can be defined as the functions that are orthogonal with respect to the inner product
can be defined as the functions that are orthogonal with respect to the inner product
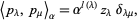 |
(7) |
where 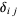 is the Kronecker delta and
is the Kronecker delta and 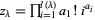 , with
, with 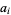 the number of occurrences of
the number of occurrences of 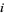 in
in 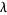 (Macdonald 1995, Dumitriu et al. 2004).
(Macdonald 1995, Dumitriu et al. 2004).
The Jack polynomial 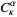 is the only homogeneous polynomial eigenfunction of the Laplace-Beltrami-type operator
is the only homogeneous polynomial eigenfunction of the Laplace-Beltrami-type operator
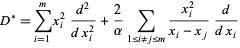 |
(8) |
with eigenvalue 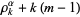 having highest-order term corresponding to
having highest-order term corresponding to 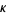 (Muirhead 1982, Dumitriu 2004). Here,
(Muirhead 1982, Dumitriu 2004). Here,
![rho_kappa^alpha=sum_(i=1)^mk_i[k_i-1-2/alpha(i-1)]](http://mathworld.wolfram.com/images/equations/JackPolynomial/NumberedEquation3.gif) |
(9) |
and 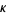 is a partition of
is a partition of 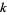 and
and 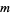 is the number of variables.
is the number of variables.
REFERENCES:
Dumitriu, I.; Edelman, A.; and Shuman, G. "MOPS: Multivariate Orthogonal Polynomials (Symbolically)." Preprint. March 26, 2004.
Foulkes, H. O. "A Survey of Some Combinatorial Aspects of Symmetric Functions." In Permutations. Paris: Gauthier-Villars, 1974.
Hua, L. K. Harmonic Analysis of Functions of Several Complex Variables in the Classical Domains. Providence, RI: Amer. Math. Soc., 1963.
Jack, H. "A Class of Symmetric Polynomials with a Parameter." Proc. Roy. Soc. Edinburgh Sec. A: Math. Phys. Sci. 69, 1-18, 1969-70.
James, A. T. "The Distribution of the Latent Roots of the Covariance Matrix." Ann. Math. Stat. 31, 151-158, 1960.
James, A. T. "Distribution of Matrix Variates and Latent Roots Derived from Normal Samples." Ann. Math. Stat. 35, 475-501, 1964.
Kadell, K. "The Selberg-Jack Polynomials." Adv. Math. 130, 33-102, 1997.
Knop, F. and Sahi, S. "A Recursion and a Combinatorial Formula for the Jack Polynomials." Invent. Math. 128, 9-22, 1997.
Lasalle, M. "Some Combinatorial Conjectures for Jack Polynomials." Ann. Combin. 2, 61-83, 1998.
Macdonald, I. G. Symmetric Functions and Hall Polynomials, 2nd ed. Oxford, England: Oxford University Press, pp. 383 and 387, 1995.
Muirhead, R. J. Aspects of Multivariate Statistical Theory. New York: Wiley, 1982.
Stanley, R. P. "Some Combinatorial Properties of Jack Symmetric Functions." Adv. in Math. 77, 76-115, 1989.
 الاكثر قراءة في التفاضل و التكامل
الاكثر قراءة في التفاضل و التكامل
 اخر الاخبار
اخر الاخبار
اخبار العتبة العباسية المقدسة

الآخبار الصحية















 قسم الشؤون الفكرية يصدر كتاباً يوثق تاريخ السدانة في العتبة العباسية المقدسة
قسم الشؤون الفكرية يصدر كتاباً يوثق تاريخ السدانة في العتبة العباسية المقدسة "المهمة".. إصدار قصصي يوثّق القصص الفائزة في مسابقة فتوى الدفاع المقدسة للقصة القصيرة
"المهمة".. إصدار قصصي يوثّق القصص الفائزة في مسابقة فتوى الدفاع المقدسة للقصة القصيرة (نوافذ).. إصدار أدبي يوثق القصص الفائزة في مسابقة الإمام العسكري (عليه السلام)
(نوافذ).. إصدار أدبي يوثق القصص الفائزة في مسابقة الإمام العسكري (عليه السلام)


















