Lambert W-Function
The Lambert 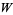 -function, also called the omega function, is the inverse function of
-function, also called the omega function, is the inverse function of
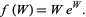 |
(1)
|
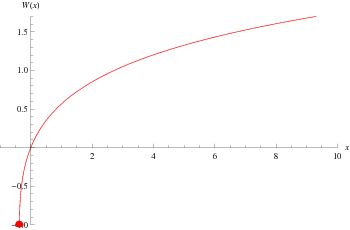
The plot above shows the function along the real axis. The principal value of the Lambert 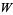 -function is implemented in the Wolfram Language as ProductLog[z]. Different branches of the function are available in the Wolfram Language as ProductLog[k, z], where
-function is implemented in the Wolfram Language as ProductLog[z]. Different branches of the function are available in the Wolfram Language as ProductLog[k, z], where 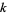 is any integer and
is any integer and 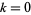 corresponds to the principal value. Although undocumented, LambertW[k, z] autoevaluates to ProductLog[k, z] in the Wolfram Language.
corresponds to the principal value. Although undocumented, LambertW[k, z] autoevaluates to ProductLog[k, z] in the Wolfram Language.
Lambert (1758) considered the solution to
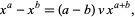 |
(2)
|
now known as Lambert's transcendental equation. Euler heard about Lambert's paper in 1764 when Lambert moved from Zurich to Berlin. After some private disputes about the priorities of some related series expansions in 1770/1771, Euler (1783) wrote a paper about Lambert's transcendental equation in which he introduced a special case which reduces to 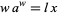 , which is nearly the definition of
, which is nearly the definition of 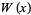 , although Euler proposed defining a function more like
, although Euler proposed defining a function more like 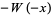 . Euler considered series solutions in this paper and, in the first paragraph, explicitly quotes Lambert as the one who first considered this equation.
. Euler considered series solutions in this paper and, in the first paragraph, explicitly quotes Lambert as the one who first considered this equation.
Eisenstein (1844) considered the series of the infinite power tower
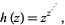 |
(3)
|
which can be expressed in closed form as
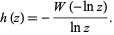 |
(4)
|
Pólya and Szegö (1925) were the first to use the symbol 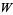 for the Lambert function.
for the Lambert function.
Banwell and Jayakumar (2000) showed that a 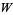 -function describes the relation between voltage, current, and resistance in a diode, and Packel and Yuen (2004) applied the
-function describes the relation between voltage, current, and resistance in a diode, and Packel and Yuen (2004) applied the 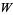 -function to a ballistic projectile in the presence of air resistance. Other applications have been discovered in statistical mechanics, quantum chemistry, combinatorics, enzyme kinetics, the physiology of vision, the engineering of thin films, hydrology, and the analysis of algorithms (Hayes 2005).
-function to a ballistic projectile in the presence of air resistance. Other applications have been discovered in statistical mechanics, quantum chemistry, combinatorics, enzyme kinetics, the physiology of vision, the engineering of thin films, hydrology, and the analysis of algorithms (Hayes 2005).
The Lambert 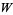 -function is illustrated above in the complex plane.
-function is illustrated above in the complex plane.

The real (left) and imaginary (right) parts of the analytic continuation of 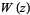 over the complex plane are illustrated above (M. Trott, pers. comm.).
over the complex plane are illustrated above (M. Trott, pers. comm.).
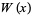 is real for
is real for 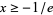 . It has the special values
. It has the special values
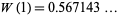 (OEIS A030178) is called the omega constant and can be considered a sort of "golden ratio" of exponentials since
(OEIS A030178) is called the omega constant and can be considered a sort of "golden ratio" of exponentials since
![exp[-W(1)]=W(1),](http://mathworld.wolfram.com/images/equations/LambertW-Function/NumberedEquation5.gif) |
(9)
|
giving
![ln[1/(W(1))]=W(1).](http://mathworld.wolfram.com/images/equations/LambertW-Function/NumberedEquation6.gif) |
(10)
|
The Lambert 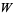 -function obeys the identity
-function obeys the identity
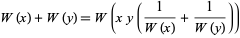 |
(11)
|
(pers. comm. from R. Corless to O. Marichev, Sep. 29, 2015).
The function 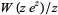 has a very complicated structure in the complex plane, but is simply equal to 1 for
has a very complicated structure in the complex plane, but is simply equal to 1 for ![R[z]>=1](http://mathworld.wolfram.com/images/equations/LambertW-Function/Inline30.gif) and a slightly extended region above and below the real axis.
and a slightly extended region above and below the real axis.
The Lambert 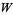 -function has the series expansion
-function has the series expansion
The Lagrange inversion theorem gives the equivalent series expansion
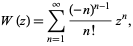 |
(14)
|
where 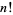 is a factorial. However, this series oscillates between ever larger positive and negative values for real
is a factorial. However, this series oscillates between ever larger positive and negative values for real 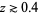 , and so cannot be used for practical numerical computation.
, and so cannot be used for practical numerical computation.
An asymptotic formula which yields reasonably accurate results for 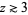 is
is
where
(Corless et al. 1996), correcting a typographical error in de Bruijn (1981). Another expansion due to Gosper (pers. comm., July 22, 1996) is the double series
![W(x)=a+sum_(n=0)^infty<span style=]() {sum_(k=0)^n(S_1(n,k))/([ln(x/a)-a]^(k-1)(n-k+1)!)}[1-(ln(x/a))/a]^n, " src="http://mathworld.wolfram.com/images/equations/LambertW-Function/NumberedEquation9.gif" style="height:51px; width:358px" /> {sum_(k=0)^n(S_1(n,k))/([ln(x/a)-a]^(k-1)(n-k+1)!)}[1-(ln(x/a))/a]^n, " src="http://mathworld.wolfram.com/images/equations/LambertW-Function/NumberedEquation9.gif" style="height:51px; width:358px" /> |
(19)
|
where 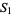 is a nonnegative Stirling number of the first kind and
is a nonnegative Stirling number of the first kind and 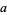 is a first approximation which can be used to select between branches. The Lambert
is a first approximation which can be used to select between branches. The Lambert 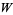 -function is two-valued for
-function is two-valued for 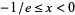 . For
. For 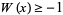 , the function is denoted
, the function is denoted 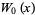 or simply
or simply 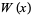 , and this is called the principal branch. For
, and this is called the principal branch. For 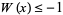 , the function is denoted
, the function is denoted 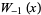 . The derivative of
. The derivative of 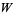 is
is
for 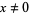 . For the principal branch when
. For the principal branch when 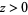 ,
,
![ln[W(z)]=lnz-W(z).](http://mathworld.wolfram.com/images/equations/LambertW-Function/NumberedEquation10.gif) |
(22)
|
The 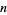 th derivatives of the Lambert
th derivatives of the Lambert 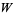 -function are given by
-function are given by
![W^((n))(z)=(W^(n-1)(z))/(z^n[1+W(z)]^(2n-1))sum_(k=1)^na_(kn)W^k(z),](http://mathworld.wolfram.com/images/equations/LambertW-Function/NumberedEquation11.gif) |
(23)
|
where 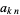 is the number triangle
is the number triangle
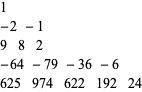 |
(24)
|
(OEIS A042977). This has exponential generating function
REFERENCES:
Banwell, T. C. and Jayakumar, A. "Exact Analytical Solution for Current Flow Through Diode with Series Resistance." Electronics Lett. 36, 291-292, 2000.
Barry, D. J., Culligen-Hensley, P. J.; and Barry, S. J. "Real Values of the  Function." ACM Trans. Math. Software 21, 161-171, 1995.
Function." ACM Trans. Math. Software 21, 161-171, 1995.
Borwein, J. M. and Corless, R. M. "Emerging Tools for Experimental Mathematics." Amer. Math. Monthly 106, 899-909, 1999.
Briggs, K. " -ology, or, Some Exactly Solvable Growth Models." http://keithbriggs.info/W-ology.html.
-ology, or, Some Exactly Solvable Growth Models." http://keithbriggs.info/W-ology.html.
Briggs, K. "Graph Theory and Lambert's  function." http://keithbriggs.info/graph_theory_and_W.html.
function." http://keithbriggs.info/graph_theory_and_W.html.
Corless, R. M. "Material on the Lambert  Function." (Ed. W. W. Küchlin). New York: ACM, pp. 197-204, 1997. http://www.apmaths.uwo.ca/~rcorless/frames/PAPERS/LambertW/.
Function." (Ed. W. W. Küchlin). New York: ACM, pp. 197-204, 1997. http://www.apmaths.uwo.ca/~rcorless/frames/PAPERS/LambertW/.
Corless, R. M.; Gonnet, G. H.; Hare, D. E. G.; Jeffrey, D. J.; and Knuth, D. E. "On the Lambert 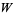 Function." Adv. Comput. Math. 5, 329-359, 1996.
Function." Adv. Comput. Math. 5, 329-359, 1996.
Corless, R. M.; Gonnet, G. H.; Hare, D. E. G.; and Jeffrey, D. J. "Lambert's 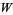 Function in Maple." Maple Technical Newsletter 9, 12-22, Spring 1993.
Function in Maple." Maple Technical Newsletter 9, 12-22, Spring 1993.
Corless, R. M. and Jeffrey, D. J. "The Wright 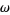 Function." In Artificial Intelligence, Automated Reasoning, and Symbolic Computation (Ed. J. Calmet, B. Benhamou, O. Caprotti, L. Henocque and V. Sorge). Berlin: Springer-Verlag, pp. 76-89, 2002.
Function." In Artificial Intelligence, Automated Reasoning, and Symbolic Computation (Ed. J. Calmet, B. Benhamou, O. Caprotti, L. Henocque and V. Sorge). Berlin: Springer-Verlag, pp. 76-89, 2002.
Corless, R. M.; Jeffrey, D. J.; and Knuth, D. E. "A Sequence of Series for the Lambert 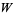 Function." In Proceedings of the 1997 International Symposium on Symbolic and Algebraic Computation, Maui, Hawaii. New York: ACM Press, pp. 197-204, 1997.
Function." In Proceedings of the 1997 International Symposium on Symbolic and Algebraic Computation, Maui, Hawaii. New York: ACM Press, pp. 197-204, 1997.
de Bruijn, N. G. Asymptotic Methods in Analysis. New York: Dover, pp. 27-28, 1981.
Eisenstein, G. "Entwicklung von 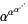 ." J. reine angew. Math. 28, 49-52, 1844.
." J. reine angew. Math. 28, 49-52, 1844.
Euler, L. "De serie Lambertina Plurimisque eius insignibus proprietatibus." Acta Acad. Scient. Petropol. 2, 29-51, 1783. Reprinted in Euler, L. Opera Omnia, Series Prima, Vol. 6: Commentationes Algebraicae. Leipzig, Germany: Teubner, pp. 350-369, 1921.
Fritsch, F. N.; Shafer, R. E.; and Crowley, W. P. "Algorithm 443: Solution of the Transcendental Equation 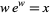 ." Comm. ACM 16, 123-124, 1973.
." Comm. ACM 16, 123-124, 1973.
Gosper, R. W. Jr. "The Solutions of 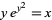 and
and 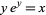 ." ACM SIGSAM Bull. 32, 8-10, 1998.
." ACM SIGSAM Bull. 32, 8-10, 1998.
Gosper, R. W. "Re: 2nd Order Eulerians." math-fun@cs.arizona.edu posting, July 22, 1996.
Gray, J. J. and Tilling, L. "Johann Heinrich Lambert, Mathematician and Scientist 1728-1777." Historia Math. 5, 13-41, 1978.
Hayes, B. "Why 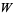 ?" Amer. Sci. 93, 104-108, 2005.
?" Amer. Sci. 93, 104-108, 2005.
Jeffrey, D. J.; Hare, D. E. G.; and Corless, R. M. "Unwinding the Branches of the Lambert 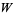 Function." Math. Scientist 21, 1-7, 1996.
Function." Math. Scientist 21, 1-7, 1996.
Jeffrey, D. J.; Hare, D. E. G.; and Corless, R. M. "Exact Rational Solutions of a Transcendental Equation." C. R. Math. Acad. Sci. Canada 20, 71-76, 1998.
Jeffrey, D. J.; Corless, R. M.; Hare, D. E. G.; and Knuth, D. E. "Sur l'inversion de 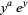 au moyen des nombres de Stirling associes." Comptes Rendus Acad. Sci. Paris 320, 1449-1452, 1995.
au moyen des nombres de Stirling associes." Comptes Rendus Acad. Sci. Paris 320, 1449-1452, 1995.
Kalman, D. "A Generalized Logarithm for Exponential-Linear Equations." College Math. J. 32, 2-14, 2001.
Lambert, J. H. "Observations variae in Mathesin Puram." Acta Helvitica, physico-mathematico-anatomico-botanico-medica 3, 128-168, 1758.
ORCCA. "The Lambert W Function." http://www.orcca.on.ca/LambertW.
Packel, E. and Yuen, D. "Projectile Motion with Resistance and the Lambert 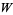 Function." College Math. J. 35, 337-350, 2004.
Function." College Math. J. 35, 337-350, 2004.
Pólya, G. and Szegö, G. Aufgaben und Lehrsätze der Analysis. Berlin, 1925. Reprinted as Problems and Theorems in Analysis I. Berlin: Springer-Verlag, 1998.
Sloane, N. J. A. Sequences A030178 and A042977 in "The On-Line Encyclopedia of Integer Sequences."
"Time for a New Elementary Function?" FOCUS: Newsletter Math. Assoc. Amer. 20, 2, Feb. 2000.
Valluri, S. R.; Jeffrey, D. J.; and Corless, R. M. "Some Applications of the Lambert  Function to Physics." Canad. J. Phys. 78, 823-831, 2000.
Function to Physics." Canad. J. Phys. 78, 823-831, 2000.
Wright, E. M. "Solution of the Equation 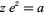 ." Bull. Amer. Math. Soc. 65, 89-93, 1959.
." Bull. Amer. Math. Soc. 65, 89-93, 1959.
 الاكثر قراءة في التفاضل و التكامل
الاكثر قراءة في التفاضل و التكامل
 اخر الاخبار
اخر الاخبار
اخبار العتبة العباسية المقدسة


