Hypergeometric Function

A generalized hypergeometric function 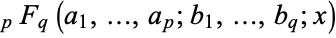 is a function which can be defined in the form of a hypergeometric series, i.e., a series for which the ratio of successive terms can be written

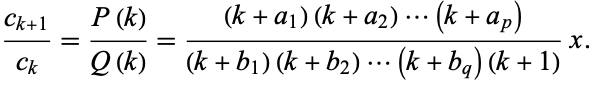(1)

(The factor of 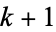 in the denominator is present for historical reasons of notation.)

The function 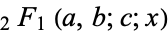 corresponding to 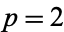,  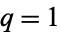is the first hypergeometric function to be studied (and, in general, arises the most frequently in physical problems), and so is frequently known as "the" hypergeometric equation or, more explicitly, Gauss's hypergeometric function (Gauss 1812, Barnes 1908). To confuse matters even more, the term "hypergeometric function" is less commonly used to mean closed form, and "hypergeometric series" is sometimes used to mean hypergeometric function.

The hypergeometric functions are solutions to the hypergeometric differential equation, which has a regular singular point at the origin. To derive the hypergeometric function from the hypergeometric differential equation

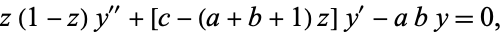(2)

use the Frobenius method to reduce it to

(3)

giving the indicial equation

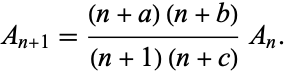(4)

Plugging this into the ansatz series

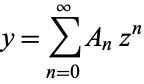(5)

then gives the solution

(6)

This is the so-called regular solution, denoted

			(7)
			(8)

which converges if 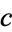 is not a negative integer (1) for all of  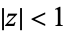and (2) on the unit circle  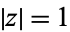if . Here, 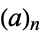 is a Pochhammer symbol.

The complete solution to the hypergeometric differential equation is

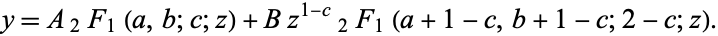(9)

The hypergeometric series is convergent for arbitrary 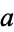, , 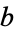and 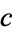 for real 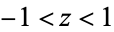, and for  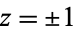if .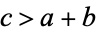

Derivatives of 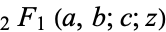 are given by

			(10)
			(11)

(Magnus and Oberhettinger 1949, p. 8).

Hypergeometric functions with special arguments reduce to elementary functions, for example,

			(12)
			(13)
			(14)
			(15)

An integral giving the hypergeometric function is

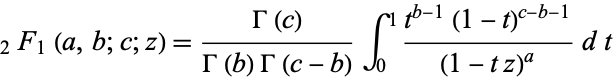(16)

as shown by Euler in 1748 (Bailey 1935, pp. 4-5). Barnes (1908) gave the contour integral

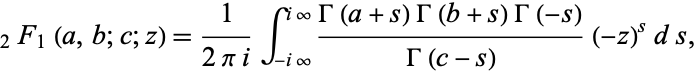(17)

where 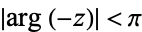 and the path is curved (if necessary) to separate the poles 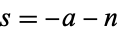, , 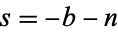... (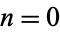, 1, ...) from the poles 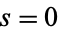, 1 ... (Bailey 1935, pp. 4-5; Whittaker and Watson 1990).

Curiously, at a number of very special points, the hypergeometric functions can assume rational,

			(18)
			(19)

(M. Trott, pers. comm., Aug. 5, 2002; Zucker and Joyce 2001), quadratic surd

			(20)
			(21)

(Zucker and Joyce 2001), and other exact values

			(22)
			(23)
			(24)

(Zucker and Joyce 2001, 2003).

An infinite family of rational values for well-poised hypergeometric functions with rational arguments is given by

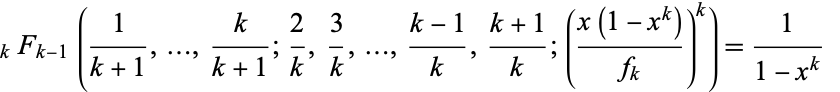(25)

for 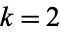, 3, ..., 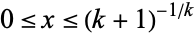, and

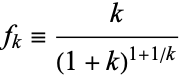(26)

(M. L. Glasser, pers. comm., Sept. 26, 2003). This gives the particular identity

(27)

for .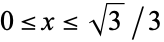

A hypergeometric function can be written using Euler's hypergeometric transformations

			(28)
			(29)
			(30)
			(31)

in any one of four equivalent forms

			(32)
			(33)
			(34)

(Abramowitz and Stegun 1972, p. 559).

It can also be written as a linear combination

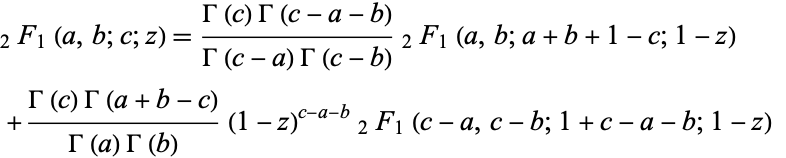(35)

(Barnes 1908; Bailey 1935, pp. 3-4; Whittaker and Watson 1990, p. 291).

Kummer found all six solutions (not necessarily regular at the origin) to the hypergeometric differential equation:

			(36)
			(37)
			(38)
			(39)
			(40)
			(41)

(Abramowitz and Stegun 1972, p. 563).

Applying Euler's hypergeometric transformations to the Kummer solutions then gives all 24 possible forms which are solutions to the hypergeometric differential equation:

			(42)
			(43)
			(44)
			(45)
			(46)
			(47)
			(48)
			(49)
			(50)
			(51)
			(52)
			(53)
			(54)
			(55)
			(56)
			(57)
			(58)
			(59)
			(60)
			(61)
			(62)
			(63)
			(64)
			(65)

(Kummer 1836; Erdélyi et al. 1981, pp. 105-106).

Goursat (1881) and Erdélyi et al. (1981) give many hypergeometric transformation formulas, including several cubic transformations.

Many functions of mathematical physics can be expressed as special cases of the hypergeometric functions. For example,

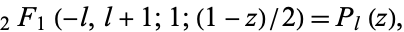(66)

where 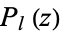 is a Legendre polynomial.

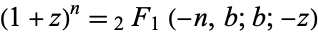(67)

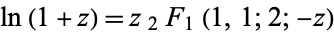(68)

Complete elliptic integrals and the Riemann P-series can also be expressed in terms of 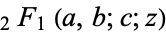. Special values include

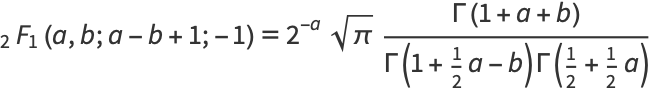	(69)
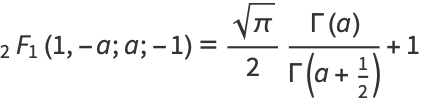	(70)
	(71)
	(72)
	(73)
	(74)

Kummer's first formula gives

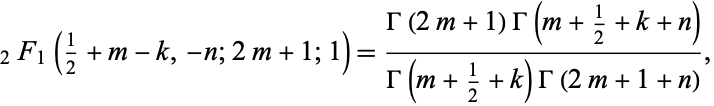(75)

where 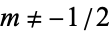, , , 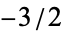.... Many additional identities are given by Abramowitz and Stegun (1972, p. 557).

Hypergeometric functions can be generalized to generalized hypergeometric functions

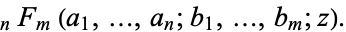(76)

A function of the form 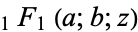 is called a confluent hypergeometric function of the first kind, and a function of the form  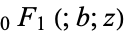is called a confluent hypergeometric limit function.

REFERENCES:

Abramowitz, M. and Stegun, I. A. (Eds.). "Hypergeometric Functions." Ch. 15 inHandbook of Mathematical Functions with Formulas, Graphs, and Mathematical Tables, 9th printing. New York: Dover, pp. 555-566, 1972.

Appell, P. and Kampé de Fériet, J. Fonctions hypergéométriques et hypersphériques: polynomes d'Hermite. Paris: Gauthier-Villars, 1926.

Arfken, G. "Hypergeometric Functions." §13.5 in Mathematical Methods for Physicists, 3rd ed. Orlando, FL: Academic Press, pp. 748-752, 1985.

Bailey, W. N. Generalised Hypergeometric Series. Cambridge, England: University Press, 1935.

Barnes, E. W. "A New Development in the Theory of the Hypergeometric Functions." Proc. London Math. Soc. 6, 141-177, 1908.

Borwein, J.; Bailey, D.; and Girgensohn, R. Experimentation in Mathematics: Computational Paths to Discovery. Wellesley, MA: A K Peters, 2004.

Emmanuel, J. "Évaluation rapide de fonctions hypergéométriques." Report RT-0242. INRIA, Jul 2000. http://www.inria.fr/rrrt/rt-0242.html.

Erdélyi, A.; Magnus, W.; Oberhettinger, F.; and Tricomi, F. G. Higher Transcendental Functions, Vol. 1. New York: Krieger, 1981.

Exton, H. Handbook of Hypergeometric Integrals: Theory, Applications, Tables, Computer Programs. Chichester, England: Ellis Horwood, 1978.

Fine, N. J. Basic Hypergeometric Series and Applications. Providence, RI: Amer. Math. Soc., 1988.

Gasper, G. and Rahman, M. Basic Hypergeometric Series. Cambridge, England: Cambridge University Press, 1990.

Gauss, C. F. "Disquisitiones Generales Circa Seriem Infinitam  etc. Pars Prior." Commentationes Societiones Regiae Scientiarum Gottingensis Recentiores, Vol. II. 1812. Reprinted in Gesammelte Werke, Bd. 3, pp. 123-163 and 207-229, 1866.

Gessel, I. and Stanton, D. "Strange Evaluations of Hypergeometric Series." SIAM J. Math. Anal. 13, 295-308, 1982.

Gosper, R. W. "Decision Procedures for Indefinite Hypergeometric Summation." Proc. Nat. Acad. Sci. USA 75, 40-42, 1978.

Goursat, M. E. "Sur l'équation différentielle linéaire qui admet pour intégrale la série hypergéométrique." Ann. Sci. École Norm. Super. Sup. 10, S3-S142, 1881.

Graham, R. L.; Knuth, D. E.; and Patashnik, O. Concrete Mathematics: A Foundation for Computer Science, 2nd ed. Reading, MA: Addison-Wesley, 1994.

Hardy, G. H. "A Chapter from Ramanujan's Note-Book." Proc. Cambridge Philos. Soc. 21, 492-503, 1923.

Hardy, G. H. "Hypergeometric Series." Ch. 7 in Ramanujan: Twelve Lectures on Subjects Suggested by His Life and Work, 3rd ed. New York: Chelsea, pp. 101-112, 1999.

Iyanaga, S. and Kawada, Y. (Eds.). "Hypergeometric Functions and Spherical Functions." Appendix A, Table 18 in Encyclopedic Dictionary of Mathematics. Cambridge, MA: MIT Press, pp. 1460-1468, 1980.

Kampé de Fériet, J. La fonction hypergéométrique. Paris: Gauthier-Villars, 1937.

Kohno, M. Global Analysis in Linear Differential Equations. Dordrecht, Netherlands: Kluwer, 1999.

Krattenthaler, C. "HYP and HYPQ." J. Symb. Comput. 20, 737-744, 1995.

Kummer, E. E. "Über die Hypergeometrische Reihe." J. reine angew. Math. 15, 39-83 and 127-172, 1836.

Magnus, W. and Oberhettinger, F. Formulas and Theorems for the Special Functions of Mathematical Physics. New York: Chelsea, 1949.

Morse, P. M. and Feshbach, H. Methods of Theoretical Physics, Part I. New York: McGraw-Hill, pp. 541-547, 1953.

Petkovšek, M.; Wilf, H. S.; and Zeilberger, D. A=B. Wellesley, MA: A K Peters, 1996. http://www.cis.upenn.edu/~wilf/AeqB.html.

Press, W. H.; Flannery, B. P.; Teukolsky, S. A.; and Vetterling, W. T. "Hypergeometric Functions." §6.12 in Numerical Recipes in FORTRAN: The Art of Scientific Computing, 2nd ed. Cambridge, England: Cambridge University Press, pp. 263-265, 1992.

Roach, K. "100,000+ Hypergeometric Formulas." http://www.planetquantum.com/HyperF/.

Seaborn, J. B. Hypergeometric Functions and Their Applications. New York: Springer-Verlag, 1991.

Snow, C. Hypergeometric and Legendre Functions with Applications to Integral Equations of Potential Theory. Washington, DC: U. S. Government Printing Office, 1952.

Spanier, J. and Oldham, K. B. "The Gauss Function 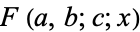." Ch. 60 in An Atlas of Functions. Washington, DC: Hemisphere, pp. 599-607, 1987.

Thomae. J. reine angew. Math. 87, 222-349, 1879.

Trott, M. "The Mathematica Guidebooks Additional Material: Rational Values of Gauss Hypergeometric Function." http://www.mathematicaguidebooks.org/additions.shtml#S_3_01.

Watson, G. N. "Ramanujan's Note Books." J. London Math. Soc. 6, 137-153, 1931.

Weisstein, E. W. "Books about Hypergeometric Functions." http://www.ericweisstein.com/encyclopedias/books/HypergeometricFunctions.html.

Whittaker, E. T. and Watson, G. N. A Course in Modern Analysis, 4th ed. Cambridge, England: Cambridge University Press, 1990.

Yoshida, M. Hypergeometric Functions, My Love: Modular Interpretations of Configuration Spaces. Braunschweig, Germany: Vieweg, 1997.

Zucker, I. J. and Joyce, G. S. "Special Values of the Hypergeometric Series II." Math. Proc. Cambridge Philos. Soc. 131, 309-319, 2001.

Zucker, I. J. and Joyce, G. S. "Special Values of The Hypergeometric Series III." Math. Proc. Cambridge Philos. Soc. 133, 213-222, 2003.