
 تاريخ الرياضيات
تاريخ الرياضيات
 الرياضيات في الحضارات المختلفة
الرياضيات في الحضارات المختلفة 
 الرياضيات المتقطعة
الرياضيات المتقطعة
 الجبر
الجبر
 الهندسة
الهندسة 
 المعادلات التفاضلية و التكاملية
المعادلات التفاضلية و التكاملية 
 التحليل
التحليل
 علماء الرياضيات
علماء الرياضيات |
Read More
Date: 14-9-2019
Date: 2-5-2019
Date: 23-6-2019
|
Gamma functions of argument 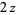 can be expressed in terms of gamma functions of smaller arguments. From the definition of the beta function,
can be expressed in terms of gamma functions of smaller arguments. From the definition of the beta function,
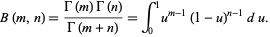 |
(1) |
Now, let 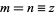 , then
, then
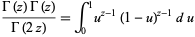 |
(2) |
and 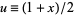 , so
, so 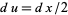 and
and
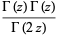 |
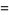 |
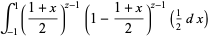 |
(3) |
 |
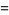 |
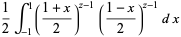 |
(4) |
 |
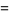 |
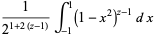 |
(5) |
 |
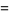 |
![2^(1-2z)[2int_0^1(1-x^2)^(z-1)dx].](http://mathworld.wolfram.com/images/equations/LegendreDuplicationFormula/Inline16.gif) |
(6) |
Now, use the beta function identity
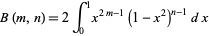 |
(7) |
to write the above as
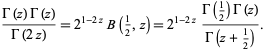 |
(8) |
Solving for 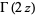 and using
and using 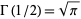 then gives
then gives
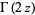 |
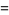 |
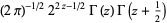 |
(9) |
 |
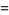 |
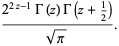 |
(10) |
REFERENCES:
Abramowitz, M. and Stegun, I. A. (Eds.). Handbook of Mathematical Functions with Formulas, Graphs, and Mathematical Tables, 9th printing. New York: Dover, p. 256, 1972.
Arfken, G. Mathematical Methods for Physicists, 3rd ed. Orlando, FL: Academic Press, pp. 561-562, 1985.
Erdélyi, A.; Magnus, W.; Oberhettinger, F.; and Tricomi, F. G. Higher Transcendental Functions, Vol. 1. New York: Krieger, p. 5, 1981.
Morse, P. M. and Feshbach, H. Methods of Theoretical Physics, Part I. New York: McGraw-Hill, pp. 424-425, 1953.



|
|
|
|
للعاملين في الليل.. حيلة صحية تجنبكم خطر هذا النوع من العمل
|
|
|
|
|
|
|
"ناسا" تحتفي برائد الفضاء السوفياتي يوري غاغارين
|
|
|
|
|
|
|
نحو شراكة وطنية متكاملة.. الأمين العام للعتبة الحسينية يبحث مع وكيل وزارة الخارجية آفاق التعاون المؤسسي
|
|
|