


 تاريخ الرياضيات
تاريخ الرياضيات
 الرياضيات في الحضارات المختلفة
الرياضيات في الحضارات المختلفة 
 الرياضيات المتقطعة
الرياضيات المتقطعة
 الجبر
الجبر
 الهندسة
الهندسة 
 المعادلات التفاضلية و التكاملية
المعادلات التفاضلية و التكاملية 
 التحليل
التحليل
 علماء الرياضيات
علماء الرياضيات |
Read More
Date: 25-8-2018
Date: 15-10-2019
Date: 12-8-2018
|
The exponent laws, also called the laws of indices (Higgens 1998) or power rules (Derbyshire 2004, p. 65), are the rules governing the combination of exponents (powers).
The laws are given by
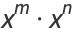 |
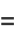 |
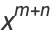 |
(1) |
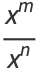 |
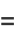 |
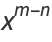 |
(2) |
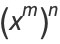 |
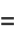 |
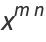 |
(3) |
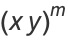 |
 |
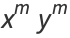 |
(4) |
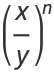 |
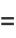 |
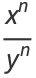 |
(5) |
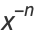 |
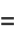 |
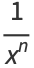 |
(6) |
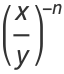 |
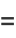 |
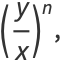 |
(7) |
where quantities in the denominator are taken to be nonzero. Special cases include
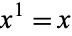 |
(8) |
and
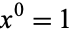 |
(9) |
for 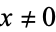 . The definition
. The definition 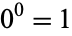 is sometimes used to simplify formulas, but it should be kept in mind that this equality is a definition and not a fundamental mathematical truth (Knuth 1992; Knuth 1997, p. 56).
is sometimes used to simplify formulas, but it should be kept in mind that this equality is a definition and not a fundamental mathematical truth (Knuth 1992; Knuth 1997, p. 56).
Note that these rules apply in general only to real quantities, and can give manifestly wrong results if they are blindly applied to complex quantities. For example,
![(i-1)^(2i)!=[(i-1)^2]^i.](http://mathworld.wolfram.com/images/equations/ExponentLaws/NumberedEquation3.gif) |
(10) |
In particular, for complex 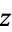 and real
and real 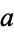 ,
,
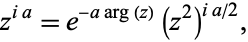 |
(11) |
where 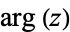 is the complex argument.
is the complex argument.
REFERENCES:
Derbyshire, J. Prime Obsession: Bernhard Riemann and the Greatest Unsolved Problem in Mathematics. New York: Penguin, 2004.
Higgins, P. M. Mathematics for the Curious. Oxford, England: Oxford University Press, 1998.
Knuth, D. E. "Two Notes on Notation." Amer. Math. Monthly 99, 403-422, 1992.
Knuth, D. E. The Art of Computer Programming, Vol. 1: Fundamental Algorithms, 3rd ed. Reading, MA: Addison-Wesley, p. 56, 1997.
Krantz, S. G. "Laws of Exponentiation." §1.2.3 in Handbook of Complex Variables. Boston, MA: Birkhäuser, p. 8, 1999.



|
|
|
|
التوتر والسرطان.. علماء يحذرون من "صلة خطيرة"
|
|
|
|
|
|
|
مرآة السيارة: مدى دقة عكسها للصورة الصحيحة
|
|
|
|
|
|
|
نحو شراكة وطنية متكاملة.. الأمين العام للعتبة الحسينية يبحث مع وكيل وزارة الخارجية آفاق التعاون المؤسسي
|
|
|