
آخر المواضيع المضافة


 تاريخ الرياضيات
تاريخ الرياضيات
 الرياضيات في الحضارات المختلفة
الرياضيات في الحضارات المختلفة 
 الرياضيات المتقطعة
الرياضيات المتقطعة
 الجبر
الجبر
 الهندسة
الهندسة 
 المعادلات التفاضلية و التكاملية
المعادلات التفاضلية و التكاملية 
 التحليل
التحليل
 علماء الرياضيات
علماء الرياضيات |
Read More
Date: 21-9-2019
Date: 10-10-2019
Date: 9-6-2019
|
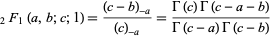 |
for ![R[c-a-b]>0](http://mathworld.wolfram.com/images/equations/GausssHypergeometricTheorem/Inline1.gif) , where
, where 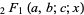 is a (Gauss) hypergeometric function. If
is a (Gauss) hypergeometric function. If 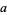 is a negative integer
is a negative integer 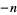 , this becomes
, this becomes
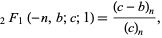 |
which is known as the Chu-Vandermonde identity.
REFERENCES:
Bailey, W. N. "Gauss's Theorem." §1.3 in Generalised Hypergeometric Series. Cambridge, England: Cambridge University Press, pp. 2-3, 1935.
Hardy, G. H. Ramanujan: Twelve Lectures on Subjects Suggested by His Life and Work, 3rd ed. New York: Chelsea, p. 104, 1999.
Koepf, W. Hypergeometric Summation: An Algorithmic Approach to Summation and Special Function Identities. Braunschweig, Germany: Vieweg, p. 31, 1998.
Petkovšek, M.; Wilf, H. S.; and Zeilberger, D. A=B. Wellesley, MA: A K Peters, pp. 42 and 126, 1996. http://www.cis.upenn.edu/~wilf/AeqB.html.



|
|
|
|
التوتر والسرطان.. علماء يحذرون من "صلة خطيرة"
|
|
|
|
|
|
|
مرآة السيارة: مدى دقة عكسها للصورة الصحيحة
|
|
|
|
|
|
|
نحو شراكة وطنية متكاملة.. الأمين العام للعتبة الحسينية يبحث مع وكيل وزارة الخارجية آفاق التعاون المؤسسي
|
|
|