


 تاريخ الرياضيات
تاريخ الرياضيات
 الرياضيات في الحضارات المختلفة
الرياضيات في الحضارات المختلفة 
 الرياضيات المتقطعة
الرياضيات المتقطعة
 الجبر
الجبر
 الهندسة
الهندسة 
 المعادلات التفاضلية و التكاملية
المعادلات التفاضلية و التكاملية 
 التحليل
التحليل
 علماء الرياضيات
علماء الرياضيات |
Read More
Date: 23-4-2019
Date: 22-4-2019
Date: 9-6-2019
|
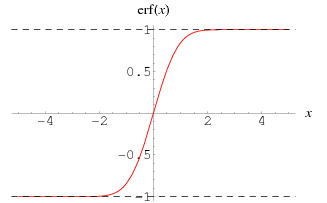
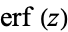 is the "error function" encountered in integrating the normal distribution (which is a normalized form of the Gaussian function). It is an entire functiondefined by
is the "error function" encountered in integrating the normal distribution (which is a normalized form of the Gaussian function). It is an entire functiondefined by
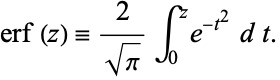 |
(1) |
Note that some authors (e.g., Whittaker and Watson 1990, p. 341) define  without the leading factor of
without the leading factor of 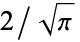 .
.
Erf is implemented in the Wolfram Language as Erf[z]. A two-argument form giving 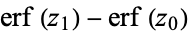 is also implemented as Erf[z0, z1].
is also implemented as Erf[z0, z1].
Erf satisfies the identities
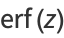 |
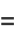 |
 |
(2) |
 |
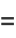 |
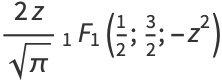 |
(3) |
 |
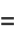 |
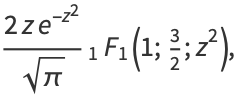 |
(4) |
where 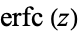 is erfc, the complementary error function, and
is erfc, the complementary error function, and 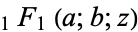 is a confluent hypergeometric function of the first kind. For
is a confluent hypergeometric function of the first kind. For 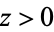 ,
,
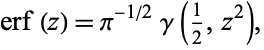 |
(5) |
where 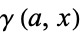 is the incomplete gamma function.
is the incomplete gamma function.
Erf can also be defined as a Maclaurin series
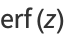 |
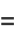 |
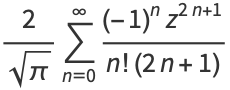 |
(6) |
 |
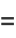 |
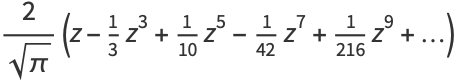 |
(7) |
(OEIS A007680). Similarly,
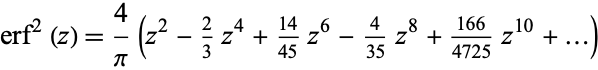 |
(8) |
(OEIS A103979 and A103980).
For 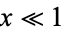 ,
, 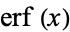 may be computed from
may be computed from
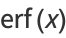 |
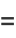 |
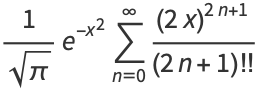 |
(9) |
 |
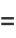 |
![2/(sqrt(pi))e^(-x^2)[x+(2x^3)/(1·3)+(4x^5)/(1·3·5)+...]](http://mathworld.wolfram.com/images/equations/Erf/Inline31.gif) |
(10) |
(OEIS A000079 and A001147; Acton 1990).
For 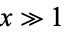 ,
,
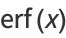 |
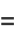 |
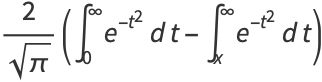 |
(11) |
 |
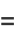 |
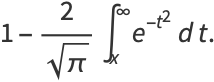 |
(12) |
Using integration by parts gives
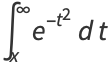 |
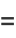 |
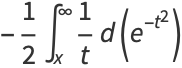 |
(13) |
 |
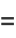 |
![-1/2[(e^(-t^2))/t]_x^infty-1/2int_x^infty(e^(-t^2)dt)/(t^2)](http://mathworld.wolfram.com/images/equations/Erf/Inline44.gif) |
(14) |
 |
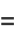 |
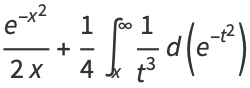 |
(15) |
 |
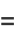 |
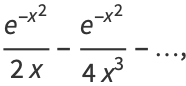 |
(16) |
so
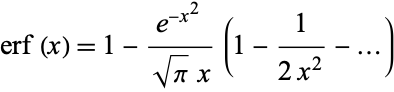 |
(17) |
and continuing the procedure gives the asymptotic series
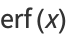 |
 |
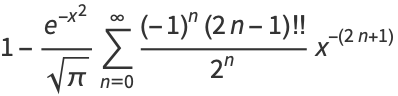 |
(18) |
 |
 |
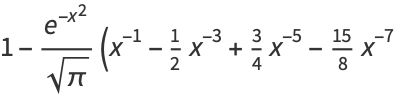 |
(19) |
 |
 |
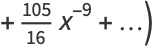 |
(20) |
(OEIS A001147 and A000079).
Erf has the values
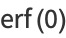 |
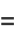 |
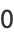 |
(21) |
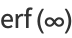 |
 |
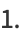 |
(22) |
It is an odd function
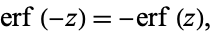 |
(23) |
and satisfies
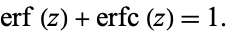 |
(24) |
Erf may be expressed in terms of a confluent hypergeometric function of the first kind 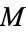 as
as
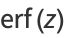 |
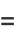 |
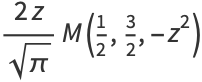 |
(25) |
 |
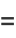 |
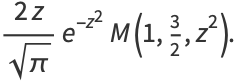 |
(26) |
Its derivative is
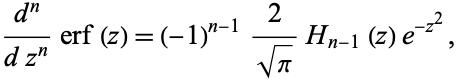 |
(27) |
where 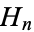 is a Hermite polynomial. The first derivative is
is a Hermite polynomial. The first derivative is
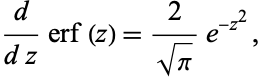 |
(28) |
and the integral is
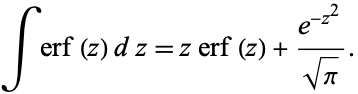 |
(29) |
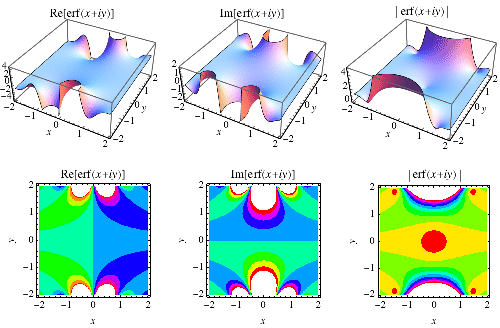 |
Erf can also be extended to the complex plane, as illustrated above.
A simple integral involving erf that Wolfram Language cannot do is given by
![int_0^pe^(-x^2)erf(p-x)dx=1/2sqrt(pi)[erf(1/2sqrt(2)p)]^2](http://mathworld.wolfram.com/images/equations/Erf/NumberedEquation10.gif) |
(30) |
(M. R. D'Orsogna, pers. comm., May 9, 2004). More complicated integrals include
![int_0^infty(e^(-(p+x)y))/(pi(p+x))sin(asqrt(x))dx=-sinh(asqrt(p))
+(e^(-asqrt(p)))/2erf(a/(2sqrt(y))-sqrt(py))+(e^(asqrt(p)))/2erf(a/(2sqrt(y))+sqrt(py))
int_0^infty(sqrt(x)e^(-(p+x)y))/(pi(p+x))cos(asqrt(x))dx=(e^(-[py+a^2/(4y)]))/(sqrt(piy))+sqrt(p)[-cosh(asqrt(p))-(e^(-asqrt(p)))/2erf(a/(2sqrt(y))-sqrt(py))+(e^(asqrt(p)))/2erf(a/(2sqrt(y))+sqrt(py))]](http://mathworld.wolfram.com/images/equations/Erf/NumberedEquation11.gif) |
(31) |
(M. R. D'Orsogna, pers. comm., Dec. 15, 2005).
Erf has the continued fraction
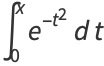 |
 |
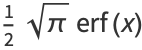 |
(32) |
 |
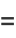 |
 |
(33) |
(Wall 1948, p. 357), first stated by Laplace in 1805 and Legendre in 1826 (Olds 1963, p. 139), proved by Jacobi, and rediscovered by Ramanujan (Watson 1928; Hardy 1999, pp. 8-9).
Definite integrals involving 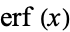 include Definite integrals involving
include Definite integrals involving 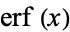 include
include
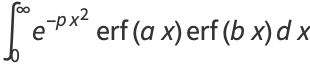 |
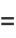 |
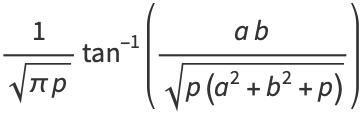 |
(34) |
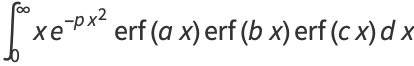 |
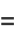 |
![1/(pip)[a/(sqrt(a^2+p))tan^(-1)((bc)/(sqrt((a^2+b^2+c^2+p)(a^2+p))))+b/(sqrt(b^2+p))tan^(-1)((ac)/(sqrt((a^2+b^2+c^2+p)(b^2+p))))+c/(sqrt(c^2+p))tan^(-1)((ab)/(sqrt((a^2+b^2+c^2+p)(c^2+p))))]](http://mathworld.wolfram.com/images/equations/Erf/Inline87.gif) |
(35) |
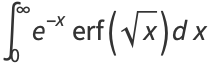 |
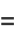 |
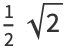 |
(36) |
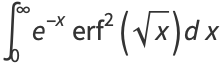 |
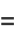 |
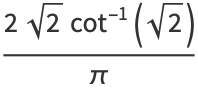 |
(37) |
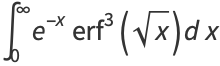 |
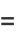 |
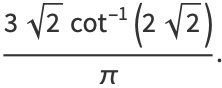 |
(38) |
The first two of these appear in Prudnikov et al. (1990, p. 123, eqns. 2.8.19.8 and 2.8.19.11), with ![R[p]>0](http://mathworld.wolfram.com/images/equations/Erf/Inline97.gif) ,
, 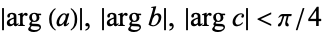 .
.
A complex generalization of 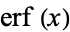 is defined as
is defined as
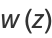 |
 |
 |
(39) |
 |
 |
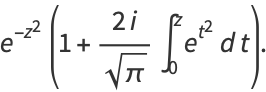 |
(40) |
Integral representations valid only in the upper half-plane ![I[z]>0](http://mathworld.wolfram.com/images/equations/Erf/Inline106.gif) are given by
are given by
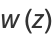 |
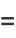 |
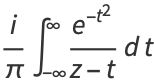 |
(41) |
 |
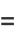 |
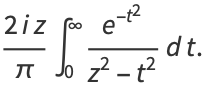 |
(42) |
REFERENCES:
Abramowitz, M. and Stegun, I. A. (Eds.). "Error Function and Fresnel Integrals." Ch. 7 in Handbook of Mathematical Functions with Formulas, Graphs, and Mathematical Tables, 9th printing. New York: Dover, pp. 297-309, 1972.
Acton, F. S. Numerical Methods That Work, 2nd printing. Washington, DC: Math. Assoc. Amer., p. 16, 1990.
Arfken, G. Mathematical Methods for Physicists, 3rd ed. Orlando, FL: Academic Press, pp. 568-569, 1985.
Hardy, G. H. Ramanujan: Twelve Lectures on Subjects Suggested by His Life and Work, 3rd ed. New York: Chelsea, 1999.
Havil, J. Gamma: Exploring Euler's Constant. Princeton, NJ: Princeton University Press, p. 105, 2003.
Olds, C. D. Continued Fractions. New York: Random House, 1963.
Prudnikov, A. P.; Brychkov, Yu. A.; and Marichev, O. I. Integrals and Series, Vol. 2: Special Functions. New York: Gordon and Breach, 1990.
Sloane, N. J. A. Sequences A000079/M1129, A001147/M3002, A007680/M2861, A103979, A103980 in "The On-Line Encyclopedia of Integer Sequences."
Spanier, J. and Oldham, K. B. "The Error Function 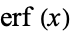 and Its Complement
and Its Complement 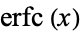 ." Ch. 40 in An Atlas of Functions. Washington, DC: Hemisphere, pp. 385-393, 1987.
." Ch. 40 in An Atlas of Functions. Washington, DC: Hemisphere, pp. 385-393, 1987.
Wall, H. S. Analytic Theory of Continued Fractions. New York: Chelsea, 1948.
Watson, G. N. "Theorems Stated by Ramanujan (IV): Theorems on Approximate Integration and Summation of Series." J. London Math. Soc. 3, 282-289, 1928.
Whittaker, E. T. and Robinson, G. "The Error Function." §92 in The Calculus of Observations: A Treatise on Numerical Mathematics, 4th ed. New York: Dover, pp. 179-182, 1967.
Whittaker, E. T. and Watson, G. N. A Course in Modern Analysis, 4th ed. Cambridge, England: Cambridge University Press, 1990.



|
|
|
|
التوتر والسرطان.. علماء يحذرون من "صلة خطيرة"
|
|
|
|
|
|
|
مرآة السيارة: مدى دقة عكسها للصورة الصحيحة
|
|
|
|
|
|
|
نحو شراكة وطنية متكاملة.. الأمين العام للعتبة الحسينية يبحث مع وكيل وزارة الخارجية آفاق التعاون المؤسسي
|
|
|