

تاريخ الرياضيات

الاعداد و نظريتها

تاريخ التحليل

تار يخ الجبر

الهندسة و التبلوجي


الرياضيات في الحضارات المختلفة

العربية

اليونانية

البابلية

الصينية

المايا

المصرية

الهندية


الرياضيات المتقطعة

المنطق

اسس الرياضيات

فلسفة الرياضيات

مواضيع عامة في المنطق


الجبر

الجبر الخطي

الجبر المجرد

الجبر البولياني

مواضيع عامة في الجبر

الضبابية

نظرية المجموعات

نظرية الزمر

نظرية الحلقات والحقول

نظرية الاعداد

نظرية الفئات

حساب المتجهات

المتتاليات-المتسلسلات

المصفوفات و نظريتها

المثلثات


الهندسة

الهندسة المستوية

الهندسة غير المستوية

مواضيع عامة في الهندسة

التفاضل و التكامل


المعادلات التفاضلية و التكاملية

معادلات تفاضلية

معادلات تكاملية

مواضيع عامة في المعادلات


التحليل

التحليل العددي

التحليل العقدي

التحليل الدالي

مواضيع عامة في التحليل

التحليل الحقيقي

التبلوجيا

نظرية الالعاب

الاحتمالات و الاحصاء

نظرية التحكم

بحوث العمليات

نظرية الكم

الشفرات

الرياضيات التطبيقية

نظريات ومبرهنات


علماء الرياضيات

500AD

500-1499

1000to1499

1500to1599

1600to1649

1650to1699

1700to1749

1750to1779

1780to1799

1800to1819

1820to1829

1830to1839

1840to1849

1850to1859

1860to1864

1865to1869

1870to1874

1875to1879

1880to1884

1885to1889

1890to1894

1895to1899

1900to1904

1905to1909

1910to1914

1915to1919

1920to1924

1925to1929

1930to1939

1940to the present

علماء الرياضيات

الرياضيات في العلوم الاخرى

بحوث و اطاريح جامعية

هل تعلم

طرائق التدريس

الرياضيات العامة

نظرية البيان
Complete Elliptic Integral of the First Kind
المؤلف:
Abramowitz, M. and Stegun, I. A.
المصدر:
Handbook of Mathematical Functions with Formulas, Graphs, and Mathematical Tables, 9th printing. New York: Dover, 1972.
الجزء والصفحة:
...
25-4-2019
4004
Complete Elliptic Integral of the First Kind
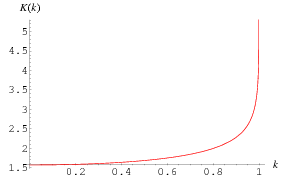
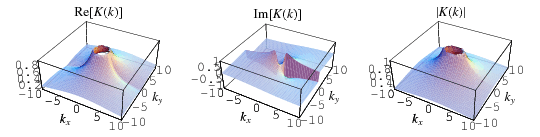
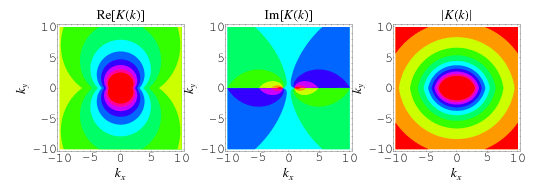
The complete elliptic integral of the first kind 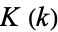 , illustrated above as a function of the elliptic modulus
, illustrated above as a function of the elliptic modulus 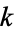 , is defined by
, is defined by
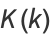 |
 |
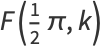 |
(1) |
 |
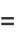 |
![pi/2sum_(n=0)^(infty)[((2n-1)!!)/((2n)!!)]^2k^(2n)](http://mathworld.wolfram.com/images/equations/CompleteEllipticIntegraloftheFirstKind/Inline8.gif) |
(2) |
 |
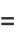 |
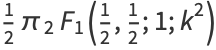 |
(3) |
where 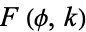 is the incomplete elliptic integral of the first kind and
is the incomplete elliptic integral of the first kind and 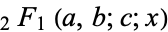 is the hypergeometric function.
is the hypergeometric function.
It is implemented in the Wolfram Language as EllipticK[m], where 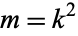 is the parameter.
is the parameter.
It satisfies the identity
 |
(4) |
where 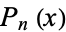 is a Legendre polynomial. This simplifies to
is a Legendre polynomial. This simplifies to
 |
(5) |
for all complex values of 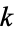 except possibly for real
except possibly for real 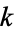 with
with 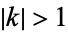 .
.
In addition, 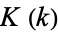 satisfies the identity
satisfies the identity
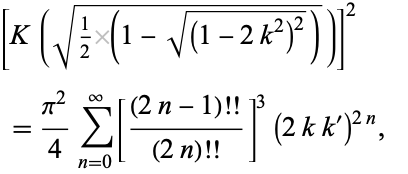 |
(6) |
where 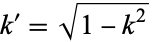 is the complementary modulus. Amazingly, this reduces to the beautiful form
is the complementary modulus. Amazingly, this reduces to the beautiful form
 |
(7) |
for 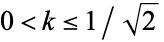 (Watson 1908, 1939).
(Watson 1908, 1939).
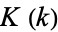 can be computed in closed form for special values of
can be computed in closed form for special values of 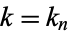 , where
, where 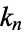 is a called an elliptic integral singular value. Other special values include
is a called an elliptic integral singular value. Other special values include
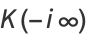 |
 |
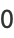 |
(8) |
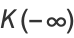 |
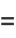 |
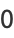 |
(9) |
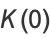 |
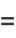 |
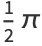 |
(10) |
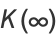 |
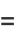 |
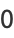 |
(11) |
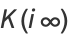 |
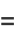 |
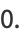 |
(12) |
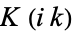 satisfies
satisfies
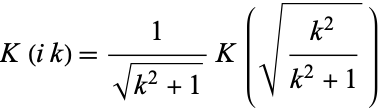 |
(13) |
possibly modulo issues of 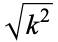 , which can be derived from equation 17.4.17 in Abramowitz and Stegun (1972, p. 593).
, which can be derived from equation 17.4.17 in Abramowitz and Stegun (1972, p. 593).
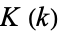 is related to the Jacobi elliptic functions through
is related to the Jacobi elliptic functions through
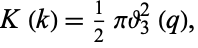 |
(14) |
where the nome is defined by
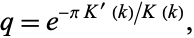 |
(15) |
with 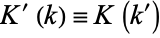 , where
, where 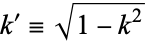 is the complementary modulus.
is the complementary modulus.
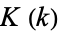 satisfies the Legendre relation
satisfies the Legendre relation
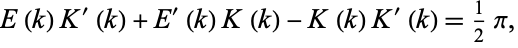 |
(16) |
where 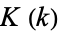 and
and 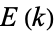 are complete elliptic integrals of the first and second kinds, respectively, and
are complete elliptic integrals of the first and second kinds, respectively, and 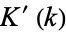 and
and 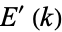 are the complementary integrals. The modulus
are the complementary integrals. The modulus 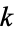 is often suppressed for conciseness, so that
is often suppressed for conciseness, so that 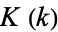 and
and 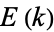 are often simply written
are often simply written 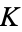 and
and 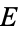 , respectively.
, respectively.
The integral 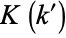 for complementary modulus is given by
for complementary modulus is given by
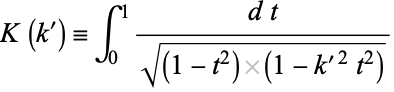 |
(17) |
(Whittaker and Watson 1990, p. 501), and
 |
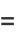 |
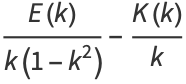 |
(18) |
 |
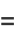 |
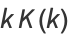 |
(19) |
(Whittaker and Watson 1990, p. 521), so
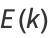 |
 |
![k(1-k^2)[(dK)/(dk)+(K(k))/k]](http://mathworld.wolfram.com/images/equations/CompleteEllipticIntegraloftheFirstKind/Inline64.gif) |
(20) |
 |
 |
![(1-k^2)[k(dK)/(dk)+K(k)]](http://mathworld.wolfram.com/images/equations/CompleteEllipticIntegraloftheFirstKind/Inline67.gif) |
(21) |
(cf. Whittaker and Watson 1990, p. 521).
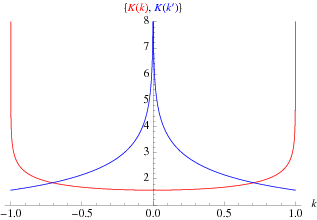
The solution to the differential equation
![d/(dk)[k(1-k^2)(dy)/(dk)]-ky=0](http://mathworld.wolfram.com/images/equations/CompleteEllipticIntegraloftheFirstKind/NumberedEquation10.gif) |
(22) |
(Zwillinger 1997, p. 122; Gradshteyn and Ryzhik 2000, p. 907) is
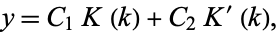 |
(23) |
where the two solutions are illustrated above and 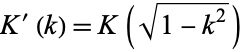 .
.
Definite integrals of 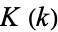 include
include
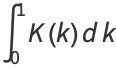 |
 |
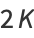 |
(24) |
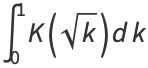 |
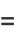 |
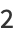 |
(25) |
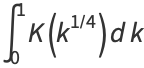 |
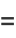 |
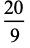 |
(26) |
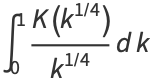 |
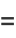 |
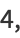 |
(27) |
where 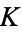 (not to be confused with
(not to be confused with 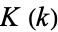 ) is Catalan's constant.
) is Catalan's constant.
REFERENCES:
Abramowitz, M. and Stegun, I. A. (Eds.). Handbook of Mathematical Functions with Formulas, Graphs, and Mathematical Tables, 9th printing. New York: Dover, 1972.
Gradshteyn, I. S. and Ryzhik, I. M. Tables of Integrals, Series, and Products, 6th ed. San Diego, CA: Academic Press, 2000.
Watson G. N. "The Expansion of Products of Hypergeometric Functions." Quart. J. Pure Appl. Math. 39, 27-51, 1907.
Watson G. N. "A Series for the Square of the Hypergeometric Function." Quart. J. Pure Appl. Math. 40, 46-57, 1908.
Watson, G. N. "Three Triple Integrals." Quart. J. Math., Oxford Ser. 2 10, 266-276, 1939.
Whittaker, E. T. and Watson, G. N. A Course in Modern Analysis, 4th ed. Cambridge, England: Cambridge University Press, 1990.
Zwillinger, D. Handbook of Differential Equations, 3rd ed. Boston, MA: Academic Press, p. 122, 1997.
 الاكثر قراءة في التفاضل و التكامل
الاكثر قراءة في التفاضل و التكامل
 اخر الاخبار
اخر الاخبار
اخبار العتبة العباسية المقدسة

الآخبار الصحية















 قسم الشؤون الفكرية يصدر كتاباً يوثق تاريخ السدانة في العتبة العباسية المقدسة
قسم الشؤون الفكرية يصدر كتاباً يوثق تاريخ السدانة في العتبة العباسية المقدسة "المهمة".. إصدار قصصي يوثّق القصص الفائزة في مسابقة فتوى الدفاع المقدسة للقصة القصيرة
"المهمة".. إصدار قصصي يوثّق القصص الفائزة في مسابقة فتوى الدفاع المقدسة للقصة القصيرة (نوافذ).. إصدار أدبي يوثق القصص الفائزة في مسابقة الإمام العسكري (عليه السلام)
(نوافذ).. إصدار أدبي يوثق القصص الفائزة في مسابقة الإمام العسكري (عليه السلام)


















