


 تاريخ الرياضيات
تاريخ الرياضيات
 الرياضيات في الحضارات المختلفة
الرياضيات في الحضارات المختلفة 
 الرياضيات المتقطعة
الرياضيات المتقطعة
 الجبر
الجبر
 الهندسة
الهندسة 
 المعادلات التفاضلية و التكاملية
المعادلات التفاضلية و التكاملية 
 التحليل
التحليل
 علماء الرياضيات
علماء الرياضيات |
Read More
Date: 10-8-2019
Date: 20-8-2018
Date: 22-5-2019
|
Elliptic alpha functions relate the complete elliptic integrals of the first 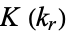 and second kinds
and second kinds 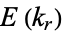 at elliptic integral singular values
at elliptic integral singular values 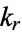 according to
according to
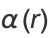 |
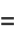 |
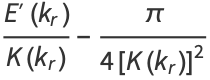 |
(1) |
 |
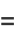 |
![pi/(4[K(k_r)]^2)+sqrt(r)-(E(k_r)sqrt(r))/(K(k_r))](http://mathworld.wolfram.com/images/equations/EllipticAlphaFunction/Inline9.gif) |
(2) |
 |
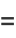 |
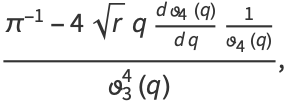 |
(3) |
where 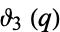 is a Jacobi theta function and
is a Jacobi theta function and
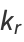 |
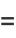 |
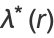 |
(4) |
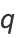 |
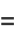 |
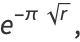 |
(5) |
and 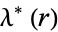 is the elliptic lambda function. The elliptic alpha function is related to the elliptic delta function by
is the elliptic lambda function. The elliptic alpha function is related to the elliptic delta function by
![alpha(r)=1/2[sqrt(r)-delta(r)].](http://mathworld.wolfram.com/images/equations/EllipticAlphaFunction/NumberedEquation1.gif) |
(6) |
It satisfies
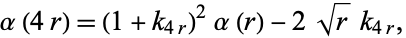 |
(7) |
and has the limit
![lim_(r->infty)[alpha(r)-1/pi] approx 8(sqrt(r)-1/pi)e^(-pisqrt(r))](http://mathworld.wolfram.com/images/equations/EllipticAlphaFunction/NumberedEquation3.gif) |
(8) |
(Borwein et al. 1989). A few specific values (Borwein and Borwein 1987, p. 172) are
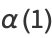 |
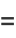 |
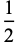 |
(9) |
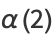 |
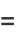 |
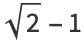 |
(10) |
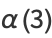 |
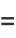 |
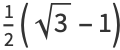 |
(11) |
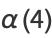 |
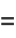 |
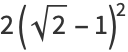 |
(12) |
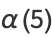 |
 |
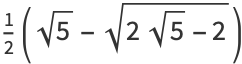 |
(13) |
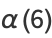 |
 |
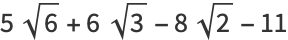 |
(14) |
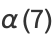 |
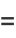 |
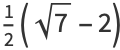 |
(15) |
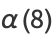 |
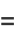 |
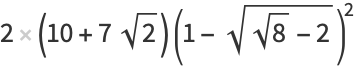 |
(16) |
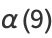 |
 |
![1/2[3-3^(3/4)sqrt(2)(sqrt(3)-1)]](http://mathworld.wolfram.com/images/equations/EllipticAlphaFunction/Inline47.gif) |
(17) |
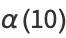 |
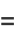 |
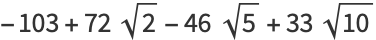 |
(18) |
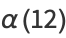 |
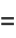 |
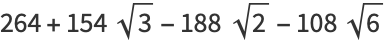 |
(19) |
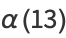 |
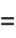 |
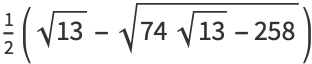 |
(20) |
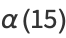 |
 |
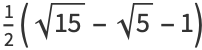 |
(21) |
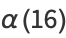 |
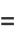 |
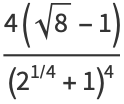 |
(22) |
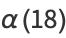 |
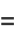 |
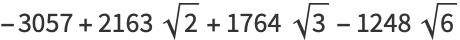 |
(23) |
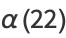 |
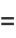 |
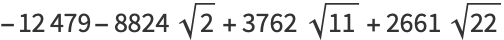 |
(24) |
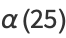 |
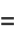 |
![5/2[1-25^(1/4)(7-3sqrt(5))]](http://mathworld.wolfram.com/images/equations/EllipticAlphaFunction/Inline71.gif) |
(25) |
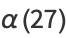 |
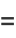 |
![3[1/2(sqrt(3)+1)-2^(1/3)]](http://mathworld.wolfram.com/images/equations/EllipticAlphaFunction/Inline74.gif) |
(26) |
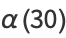 |
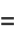 |
![1/2{sqrt(30)-(2+sqrt(5))^2(3+sqrt(10))^2×(-6-5sqrt(2)-3sqrt(5)-2sqrt(10)+sqrt(6)sqrt(57+40sqrt(2)))×[56+38sqrt(2)+sqrt(30)(2+sqrt(5))(3+sqrt(10))]}](http://mathworld.wolfram.com/images/equations/EllipticAlphaFunction/Inline77.gif) |
(27) |
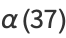 |
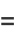 |
![1/2[sqrt(37)-(171-25sqrt(37))sqrt(sqrt(37)-6)]](http://mathworld.wolfram.com/images/equations/EllipticAlphaFunction/Inline80.gif) |
(28) |
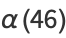 |
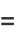 |
![1/2[sqrt(46)+(18+13sqrt(2)+sqrt(661+468sqrt(2)))^2×(18+13sqrt(2)-3sqrt(2)sqrt(147+104sqrt(2))+sqrt(661+468sqrt(2)))×(200+14sqrt(2)+26sqrt(23)+18sqrt(46)+sqrt(46)sqrt(661+468sqrt(2)))]](http://mathworld.wolfram.com/images/equations/EllipticAlphaFunction/Inline83.gif) |
(29) |
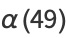 |
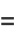 |
![7/2-sqrt(7[sqrt(2)7^(3/4)(33011+12477sqrt(7))-21(9567+3616sqrt(7))])](http://mathworld.wolfram.com/images/equations/EllipticAlphaFunction/Inline86.gif) |
(30) |
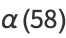 |
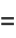 |
![[1/2(sqrt(29)+5)]^6(99sqrt(29)-444)(99sqrt(2)-70-13sqrt(29))](http://mathworld.wolfram.com/images/equations/EllipticAlphaFunction/Inline89.gif) |
(31) |
 |
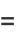 |
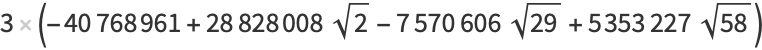 |
(32) |
 |
 |
![(8[2(sqrt(8)-1)-(2^(1/4)-1)^4])/((sqrt(sqrt(2)+1)+2^(5/8))^4).](http://mathworld.wolfram.com/images/equations/EllipticAlphaFunction/Inline95.gif) |
(33) |
J. Borwein has written an algorithm which uses lattice basis reduction to provide algebraic values for 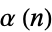 .
.
REFERENCES:
Borwein, J. M. and Borwein, P. B. Pi & the AGM: A Study in Analytic Number Theory and Computational Complexity. New York: Wiley, 1987.
Borwein, J. M.; Borwein, P. B.; and Bailey, D. H. "Ramanujan, Modular Equations, and Approximations to Pi, or How to Compute One Billion Digits of Pi." Amer. Math. Monthly 96, 201-219, 1989.



|
|
|
|
15 نوعا من الأطعمة تساعدك على ترطيب جسمك خلال موجة الحر
|
|
|
|
|
|
|
"ناسا" تختار شركة "سبيس إكس" لـ"مهمة خاصة" في 2030
|
|
|
|
|
|
|
بالصور: بمناسبة عيد الغدير الاغر.. قراءة خطبة النبي الأكرم (ص وآله) بالمسلمين في يوم (غدير خم)
|
|
|