


 تاريخ الرياضيات
تاريخ الرياضيات
 الرياضيات في الحضارات المختلفة
الرياضيات في الحضارات المختلفة 
 الرياضيات المتقطعة
الرياضيات المتقطعة
 الجبر
الجبر
 الهندسة
الهندسة 
 المعادلات التفاضلية و التكاملية
المعادلات التفاضلية و التكاملية 
 التحليل
التحليل
 علماء الرياضيات
علماء الرياضيات |
Read More
Date: 31-8-2019
Date: 28-8-2018
Date: 25-4-2019
|
Suppose 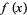 is a function of
is a function of  that is twice differentiable at a stationary point
that is twice differentiable at a stationary point 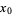 .
.
1. If 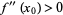 , then
, then 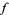 has a local minimum at
has a local minimum at 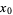 .
.
2. If 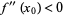 , then
, then 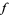 has a local maximum at
has a local maximum at 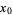 .
.
The extremum test gives slightly more general conditions under which a function with 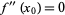 is a maximum or minimum.
is a maximum or minimum.
If 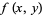 is a two-dimensional function that has a local extremum at a point
is a two-dimensional function that has a local extremum at a point 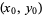 and has continuous partial derivatives at this point, then
and has continuous partial derivatives at this point, then 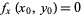 and
and 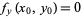 . The second partial derivatives test classifies the point as a local maximum or local minimum.
. The second partial derivatives test classifies the point as a local maximum or local minimum.
Define the second derivative test discriminant as
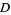 |
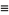 |
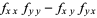 |
(1) |
 |
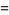 |
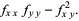 |
(2) |
Then
1. If 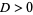 and
and 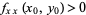 , the point is a local minimum.
, the point is a local minimum.
2. If 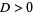 and
and 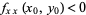 , the point is a local maximum.
, the point is a local maximum.
3. If 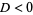 , the point is a saddle point.
, the point is a saddle point.
4. If 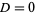 , higher order tests must be used.
, higher order tests must be used.
REFERENCES:
Abramowitz, M. and Stegun, I. A. (Eds.). Handbook of Mathematical Functions with Formulas, Graphs, and Mathematical Tables, 9th printing. New York: Dover, p. 14, 1972.
Thomas, G. B. Jr. and Finney, R. L. "Maxima, Minima, and Saddle Points." §12.8 in Calculus and Analytic Geometry, 8th ed. Reading, MA: Addison-Wesley, pp. 881-891, 1992.



|
|
|
|
"عادة ليلية" قد تكون المفتاح للوقاية من الخرف
|
|
|
|
|
|
|
ممتص الصدمات: طريقة عمله وأهميته وأبرز علامات تلفه
|
|
|
|
|
|
|
المجمع العلمي للقرآن الكريم يقيم جلسة حوارية لطلبة جامعة الكوفة
|
|
|