المرجع الألكتروني للمعلوماتية
القرآن الكريم وعلومه
العقائد الإسلامية
الفقه وأصوله 
الرجال والحديث 
سيرة الرسول وآله 
علوم اللغة العربية 
الأدب العربي 
الأسرة والمجتمع 
الأخلاق والأدعية 
التاريخ 
الادارة والاقتصاد 
علم الفيزياء 
علم الكيمياء 
علم الأحياء 
الرياضيات 
الهندسة المدنية 
الزراعة 
الجغرافية 
القانون 
اللغة الأنكليزية 
الأخبار 
الإعلام 
مكتبة الصور 
أقلام بمختلف الألوان 
إضاءات
مفتاح
أجوبة الإستفتاءات الشرعية
وثائقيات
تاريخ الرياضيات
الرياضيات في الحضارات المختلفة
الرياضيات المتقطعة
الجبر
الهندسة
المعادلات التفاضلية و التكاملية
التحليل
علماء الرياضيات | Serret,s Integral |
 1632
 02:07 مساءً
date: 25-8-2018 |
Author : Boros, G. and Moll, V. 
Book or Source : Irresistible Integrals: Symbolics, Analysis and Experiments in the Evaluation of Integrals. Cambridge, England: Cambridge University Press, 2004. 
Page and Part : ...|
Read More
Date: 30-3-2019
2918
Date: 29-7-2019
1531
Date: 12-10-2018
1612
|
Serret's integral is given by
 |
 |
 |
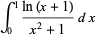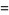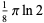(1) |
 |
 |
 |
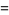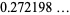(2) |
(OEIS A102886; Serret 1844; Gradshteyn and Ryzhik 2000, eqn. 4.291.8; Boros and Moll 2004, p. 243).
REFERENCES:
Boros, G. and Moll, V. Irresistible Integrals: Symbolics, Analysis and Experiments in the Evaluation of Integrals. Cambridge, England: Cambridge University Press, 2004.
Gradshteyn, I. S. and Ryzhik, I. M. Tables of Integrals, Series, and Products, 6th ed. San Diego, CA: Academic Press, 2000.
Serret, M. J. A. "Sur l'intégrale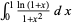 
." J. Math. Pures Appl. 9, 436, 1844.
Sloane, N. J. A. Sequence A102886 in "The On-Line Encyclopedia of Integer Sequences."
|
|
|
|
"عادة ليلية" قد تكون المفتاح للوقاية من الخرف
|
|
|
|
|
|
|
ممتص الصدمات: طريقة عمله وأهميته وأبرز علامات تلفه
|
|
|
|
|
|
|
المجمع العلمي للقرآن الكريم يقيم جلسة حوارية لطلبة جامعة الكوفة
|
|
|
