المرجع الألكتروني للمعلوماتية
القرآن الكريم وعلومه
العقائد الإسلامية
الفقه وأصوله 
الرجال والحديث 
سيرة الرسول وآله 
علوم اللغة العربية 
الأدب العربي 
الأسرة والمجتمع 
الأخلاق والأدعية 
التاريخ 
الادارة والاقتصاد 
علم الفيزياء 
علم الكيمياء 
علم الأحياء 
الرياضيات 
الهندسة المدنية 
الزراعة 
الجغرافية 
القانون 
اللغة الأنكليزية 
الأخبار 
الإعلام 
مكتبة الصور 
أقلام بمختلف الألوان 
إضاءات
مفتاح
أجوبة الإستفتاءات الشرعية
وثائقيات
تاريخ الرياضيات
الرياضيات في الحضارات المختلفة
الرياضيات المتقطعة
الجبر
الهندسة
المعادلات التفاضلية و التكاملية
التحليل
علماء الرياضيات | Melnikov-Arnold Integral |
 1848
 01:46 مساءً
date: 23-8-2018 |
Author : Chirikov, B. V 
Book or Source : A Universal Instability of Many-Dimensional Oscillator Systems." Phys. Rep. 52 
Page and Part : 264-379|
Read More
Date: 8-8-2019
1552
Date: 7-9-2019
2623
Date: 8-9-2019
2215
|
![A_m(lambda)=int_(-infty)^inftycos[1/2mphi(t)-lambdat]dt,](http://mathworld.wolfram.com/images/equations/Melnikov-ArnoldIntegral/NumberedEquation1.gif) |
(1) |
where the function
 |
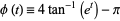(2) |
describes the motion along the pendulum separatrix. Chirikov (1979) has shown that this integral has the approximate value
 |
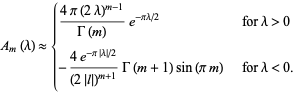(3) |
REFERENCES:
Chirikov, B. V. "A Universal Instability of Many-Dimensional Oscillator Systems." Phys. Rep. 52, 264-379, 1979.
|
|
|
|
دخلت غرفة فنسيت ماذا تريد من داخلها.. خبير يفسر الحالة
|
|
|
|
|
|
|
ثورة طبية.. ابتكار أصغر جهاز لتنظيم ضربات القلب في العالم
|
|
|
|
|
|
|
العتبة العباسية المقدسة تقدم دعوة لجامعة سومر للمشاركة في حفل التخرج المركزي الخامس
|
|
|
