المرجع الألكتروني للمعلوماتية
القرآن الكريم وعلومه
العقائد الإسلامية
الفقه وأصوله 
الرجال والحديث 
سيرة الرسول وآله 
علوم اللغة العربية 
الأدب العربي 
الأسرة والمجتمع 
الأخلاق والأدعية 
التاريخ 
الادارة والاقتصاد 
علم الفيزياء 
علم الكيمياء 
علم الأحياء 
الرياضيات 
الهندسة المدنية 
الزراعة 
الجغرافية 
القانون 
اللغة الأنكليزية 
الأخبار 
الإعلام 
مكتبة الصور 
أقلام بمختلف الألوان 
إضاءات
مفتاح
أجوبة الإستفتاءات الشرعية
وثائقيات
تاريخ الرياضيات
الرياضيات في الحضارات المختلفة
الرياضيات المتقطعة
الجبر
الهندسة
المعادلات التفاضلية و التكاملية
التحليل
علماء الرياضيات | Cavalieri,s Quadrature Formula |
 1546
 05:55 مساءً
date: 18-8-2018 |
Author : Bradley, D. M 
Book or Source : "A Remark on Cavalieri,s Quadrature Formula." Amer. Math. Monthly 110, 437, 2003. 
Page and Part : ...|
Read More
Date: 6-8-2019
4676
Date: 24-3-2019
1346
Date: 22-5-2019
1654
|
The definite integral
 |
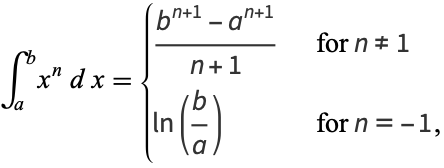(1) |
where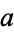 
, 
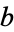, and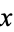 
are real numbers and 
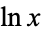is the natural logarithm.
REFERENCES:
Bradley, D. M. "A Remark on Cavalieri's Quadrature Formula." Amer. Math. Monthly 110, 437, 2003.
Wildberger, N. J. "A New Proof of Cavalieri's Quadrature Formula." Amer. Math. Monthly 109, 843-845, 2002.
|
|
|
|
كل ما تود معرفته عن أهم فيتامين لسلامة الدماغ والأعصاب
|
|
|
|
|
|
|
ماذا سيحصل للأرض إذا تغير شكل نواتها؟
|
|
|
|
|
|
|
جامعة الكفيل تناقش تحضيراتها لإطلاق مؤتمرها العلمي الدولي السادس
|
|
|
