A formal extension of the hypergeometric function to two variables, resulting in four kinds of functions (Appell 1925; Picard 1880ab, 1881; Goursat 1882; Whittaker and Watson 1990, Ex. 22, p. 300),

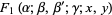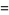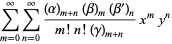			(1)
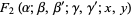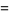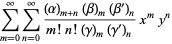			(2)
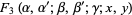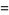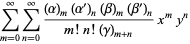			(3)
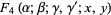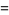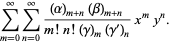			(4)

These double series are absolutely convergent for

{F_1 for |x|<1,|y|<1; F_2 for |x|+|y|<1; F_3 for |x|<1,|y|<1; F_4 for |x|^(1/2)+|y|^(1/2)<1. " src="http://mathworld.wolfram.com/images/equations/AppellHypergeometricFunction/NumberedEquation1.gif" style="height:86px; width:157px" />

(5)

Appell defined the functions in 1880 and they were subsequently studied by Picard in 1881. The functions 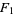, , 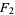and 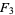 can be expressed in terms of double integrals as

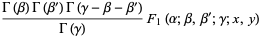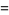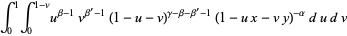			(6)
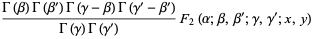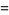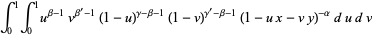			(7)
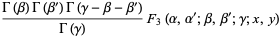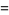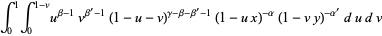			(8)

(Bailey 1934, pp. 76-77). There appears to be no simple integral representation of this type for the function 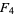 (Bailey 1934, p. 77).

The function 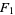 can also be expressed by the simple integral

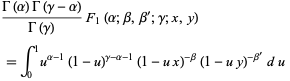(9)

(Bailey 1934, p. 77), for  and .

The Appell functions are special cases of the Kampé de Fériet function, and are the first four in the set of Horn functions. The 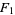 function is implemented in the Wolfram Language as AppellF1[a, b1, b2, c, x, y].

For general complex parameters, the 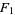 function can be written as the contour integral

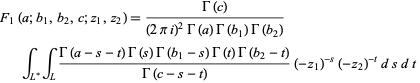(10)

for 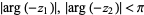, where  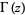is a gamma function 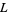and  and 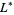 are complicated contours related to those used in the definition of theMeijer G-function. In fact, the four functions can also be expressed as double contour integrals taken along contours of the Barnes type (Bailey 1934).

In particular, the general integral

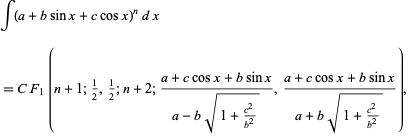(11)

where

(12)

has a closed form in terms of .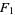

Integrals that result in particularly nice closed forms involving the 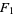 function include

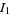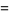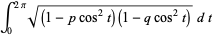			(13)
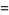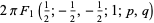			(14)
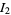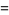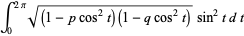			(15)
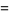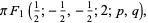			(16)

which arise in computing area and geometric centroid of the interior of the cranioid curve.

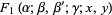 reduces to the hypergeometric function in the cases

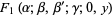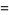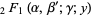			(17)
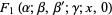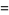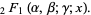			(18)

In addition,

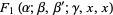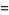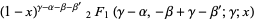			(19)
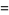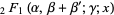			(20)
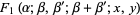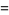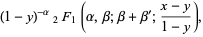			(21)

where 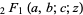 is a hypergeometric function.

REFERENCES:

Appell, P. "Sur les fonctions hypergéométriques de plusieurs variables." In Mémoir. Sci. Math. Paris: Gauthier-Villars, 1925.

Appell, P. and Kampé de Fériet, J. Fonctions hypergéométriques et hypersphériques: polynomes d'Hermite. Paris: Gauthier-Villars, 1926.

Bailey, W. N. "A Reducible Case of the Fourth Type of Appell's Hypergeometric Functions of Two Variables." Quart. J. Math. (Oxford) 4, 305-308, 1933.

Bailey, W. N. "On the Reducibility of Appell's Function 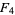." Quart. J. Math. (Oxford) 5, 291-292, 1934.

Bailey, W. N. "Appell's Hypergeometric Functions of Two Variables." Ch. 9 in Generalised Hypergeometric Series. Cambridge, England: Cambridge University Press, pp. 73-83 and 99-101, 1935.

Erdélyi, A.; Magnus, W.; Oberhettinger, F.; and Tricomi, F. G. Higher Transcendental Functions, Vol. 1. New York: Krieger, pp. 222 and 224, 1981.

Exton, H. Handbook of Hypergeometric Integrals: Theory, Applications, Tables, Computer Programs. Chichester, England: Ellis Horwood, p. 27, 1978.

Goursat, E. "Extension du problème de Riemann à des fonctions hypergéométriques de deux variables." Comptes Rendus Acad. Sci. Paris 95, 903 and 1044, 1882.

Iyanaga, S. and Kawada, Y. (Eds.). Encyclopedic Dictionary of Mathematics. Cambridge, MA: MIT Press, p. 1461, 1980.

Picard, E. "Sur une classe de fonctions de deux variables indépendantes." Comptes Rendus Acad. Sci. Paris 90, 1119-1121, 1880a.

Picard, E. "Sur une extension aux fonctions de deux variables du problème de Riemann relatif aux fonctions hypergéométriques." Comptes Rendus Acad. Sci. Paris 90, 1267-1269, 1880b.

Picard, E. "Sur une extension aux fonctions de deux variables du problème de Riemann relatif aux fonctions hypergéométriques." Ann. Ecole Norm. Sup. (2) 10, 305-322, 1881.

Watson, G. N. "The Product of Two Hypergeometric Functions." Proc. London Math. Soc. 20, 189-195, 1922.

Whittaker, E. T. and Watson, G. N. A Course in Modern Analysis, 4th ed. Cambridge, England: Cambridge University Press, 1990.

اخر الاخبار

اخبار العتبة العباسية المقدسة

العتبة العباسية المقدسة تواصل تنظيم مجالس العزاء الصباحية بذكرى زيارة عاشوراء

مواكب العزاء تستذكر في التاسع من شهر المحرم شهادة عبدالله الرضيع بن الحسين (عليهما السلام)

العتبة العباسية المقدسة تستذكر تضحيات القاسم بن الحسن (عليهما السلام)

شعبة الحرم الشريف تواصل تنفيذ خطتها الخاصة بشهر المحرّم داخل مرقد أبي الفضل العباس (عليه السلام)

المزيد

الآخبار الصحية

لهذا السبب.. إغلاق 25 مركزًا لعلاج الإدمان في مصر ؟

خلافا للاعتقاد الشائع.. علماء يكشفون أسرار بذور البطيخ ؟!

هذا ما يحدث لجسمك عند تناولك الطماطم بانتظام !

تعرف على أطعمة تسرّع "تعافي الجسم" من حروق الشمس

المزيد

الآخبار التكنلوجية

الثلوج تغطي الصحراء الأكثر جفافا في العالم!

بتلسكوب "ألما".. التقاط صورا غير مسبوقة لبدايات الكون !

هل هاتفك مراقب؟.. 5 علامات خطيرة تكشف التجسس عليك

دبي تطلق أول رحلة تجريبية للتاكسي الجوي

المزيد