Sturm-Liouville Equation

A second-order ordinary differential equation

where 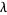 is a constant and  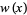is a known function called either the density or weighting function. The solutions (with appropriate boundary conditions) of  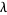are called eigenvalues and the corresponding  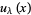eigenfunctions. The solutions of this equation satisfy important mathematical properties under appropriate boundary conditions (Arfken 1985).

There are many approaches to solving Sturm-Liouville problems in the Wolfram Language. Probably the most straightforward approach is to use variational (or Galerkin) methods. For example, VariationalBound in the Wolfram Language package VariationalMethods` and NVariationalBound give approximate eigenvalues and eigenfunctions.

Trott (2006, pp. 337-388) outlines the inverse Sturm-Liouville problem.

REFERENCES:

Arfken, G. "Sturm-Liouville Theory--Orthogonal Functions." Ch. 9 in Mathematical Methods for Physicists, 3rd ed. Orlando, FL: Academic Press, pp. 497-538, 1985.

Trott, M. The Mathematica GuideBook for Symbolics. New York: Springer-Verlag, 2006. http://www.mathematicaguidebooks.org/.