المرجع الألكتروني للمعلوماتية
القرآن الكريم وعلومه
العقائد الإسلامية
الفقه وأصوله 
الرجال والحديث 
سيرة الرسول وآله 
علوم اللغة العربية 
الأدب العربي 
الأسرة والمجتمع 
الأخلاق والأدعية 
التاريخ 
الادارة والاقتصاد 
علم الفيزياء 
علم الكيمياء 
علم الأحياء 
الرياضيات 
الهندسة المدنية 
الزراعة 
الجغرافية 
القانون 
اللغة الأنكليزية 
الأخبار 
الإعلام 
مكتبة الصور 
أقلام بمختلف الألوان 
إضاءات
مفتاح
أجوبة الإستفتاءات الشرعية
وثائقيات
تاريخ الرياضيات
الرياضيات في الحضارات المختلفة
الرياضيات المتقطعة
الجبر
الهندسة
المعادلات التفاضلية و التكاملية
التحليل
علماء الرياضيات | Hypergeometric Differential Equation |
 675
 01:59 مساءً
date: 13-6-2018 |
Author : Bailey, W. N 
Book or Source : Generalised Hypergeometric Series. Cambridge, England: University Press 
Page and Part : ...|
Read More
Date: 22-5-2018
723
Date: 11-6-2018
1044
Date: 22-6-2018
519
|
/(dz)-aby=0.](http://mathworld.wolfram.com/images/equations/HypergeometricDifferentialEquation/NumberedEquation1.gif) |
It has regular singular points at 0, 1, and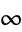 
. Every second-order ordinary differential equation with at most three regular singular points can be transformed into the hypergeometric differential equation.
REFERENCES:
Bailey, W. N. Generalised Hypergeometric Series. Cambridge, England: University Press, pp. 1-2, 1935.
Morse, P. M. and Feshbach, H. Methods of Theoretical Physics, Part I. New York: McGraw-Hill, pp. 542-543, 1953.
Zwillinger, D. Handbook of Differential Equations, 3rd ed. Boston, MA: Academic Press, p. 123, 1997.
|
|
|
|
5 علامات تحذيرية قد تدل على "مشكل خطير" في الكبد
|
|
|
|
|
|
|
اللجنتان العلمية والتحضيرية تناقش ملخصات الأبحاث المقدمة لمؤتمر العميد العالمي السابع
|
|
|
