المرجع الألكتروني للمعلوماتية
القرآن الكريم وعلومه
العقائد الإسلامية
الفقه وأصوله 
الرجال والحديث 
سيرة الرسول وآله 
علوم اللغة العربية 
الأدب العربي 
الأسرة والمجتمع 
الأخلاق والأدعية 
التاريخ 
الادارة والاقتصاد 
علم الفيزياء 
علم الكيمياء 
علم الأحياء 
الرياضيات 
الهندسة المدنية 
الزراعة 
الجغرافية 
القانون 
اللغة الأنكليزية 
الأخبار 
الإعلام 
مكتبة الصور 
أقلام بمختلف الألوان 
إضاءات
مفتاح
أجوبة الإستفتاءات الشرعية
وثائقيات
تاريخ الرياضيات
الرياضيات في الحضارات المختلفة
الرياضيات المتقطعة
الجبر
الهندسة
المعادلات التفاضلية و التكاملية
التحليل
علماء الرياضيات | Lamé,s Differential Equation Types |
 848
 03:08 مساءً
date: 22-6-2018 |
Author : Whittaker, E. T. and Watson 
Book or Source : A Course in Modern Analysis, 4th ed. Cambridge, England: Cambridge University Press, 1990. 
Page and Part : ...|
Read More
Date: 27-12-2018
595
Date: 3-7-2018
741
Date: 11-6-2018
1234
|
Whittaker and Watson (1990, pp. 539-540) write Lamé's differential equation for ellipsoidal harmonics of the first kindof the four types as
![4delta(theta)d/(dtheta)[f(theta)(dlambda(theta))/(dtheta)]](http://mathworld.wolfram.com/images/equations/LamesDifferentialEquationTypes/Inline1.gif) |
 |
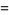![[2m(2m+1)theta+c]lambda(theta)](http://mathworld.wolfram.com/images/equations/LamesDifferentialEquationTypes/Inline3.gif) |
(1) |
![4delta(theta)d/(dtheta)[f(theta)(dlambda(theta))/(dtheta)]](http://mathworld.wolfram.com/images/equations/LamesDifferentialEquationTypes/Inline4.gif) |
 |
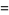![[(2m+1)(2m+2)theta+c]lambda(theta)](http://mathworld.wolfram.com/images/equations/LamesDifferentialEquationTypes/Inline6.gif) |
(2) |
![4delta(theta)d/(dtheta)[f(theta)(dlambda(theta))/(dtheta)]](http://mathworld.wolfram.com/images/equations/LamesDifferentialEquationTypes/Inline7.gif) |
 |
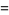![[(2m+2)(2m+3)theta+c]lambda(theta)](http://mathworld.wolfram.com/images/equations/LamesDifferentialEquationTypes/Inline9.gif) |
(3) |
![4delta(theta)d/(dtheta)[f(theta)(dlambda(theta))/(dtheta)]](http://mathworld.wolfram.com/images/equations/LamesDifferentialEquationTypes/Inline10.gif) |
 |
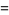![[(2m+3)(2m+4)theta+c]lambda(theta),](http://mathworld.wolfram.com/images/equations/LamesDifferentialEquationTypes/Inline12.gif) |
(4) |
where
 |
 |
 |
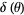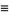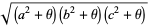(5) |
 |
 |
 |
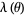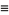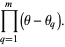(6) |
REFERENCES:
Whittaker, E. T. and Watson, G. N. A Course in Modern Analysis, 4th ed. Cambridge, England: Cambridge University Press, 1990.
|
|
|
|
"عادة ليلية" قد تكون المفتاح للوقاية من الخرف
|
|
|
|
|
|
|
ممتص الصدمات: طريقة عمله وأهميته وأبرز علامات تلفه
|
|
|
|
|
|
|
المجمع العلمي للقرآن الكريم يقيم جلسة حوارية لطلبة جامعة الكوفة
|
|
|
