
آخر المواضيع المضافة


 تاريخ الرياضيات
تاريخ الرياضيات
 الرياضيات في الحضارات المختلفة
الرياضيات في الحضارات المختلفة 
 الرياضيات المتقطعة
الرياضيات المتقطعة
 الجبر
الجبر
 الهندسة
الهندسة 
 المعادلات التفاضلية و التكاملية
المعادلات التفاضلية و التكاملية 
 التحليل
التحليل
 علماء الرياضيات
علماء الرياضيات |
Read More
Date: 5-7-2018
Date: 3-7-2018
Date: 27-12-2018
|
The second-order ordinary differential equation
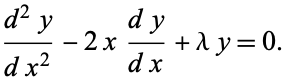 |
(1) |
This differential equation has an irregular singularity at 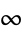 . It can be solved using the series method
. It can be solved using the series method
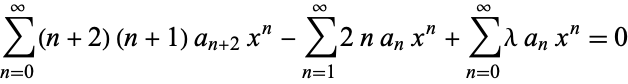 |
(2) |
![(2a_2+lambdaa_0)+sum_(n=1)^infty[(n+2)(n+1)a_(n+2)-2na_n+lambdaa_n]x^n=0.](http://mathworld.wolfram.com/images/equations/HermiteDifferentialEquation/NumberedEquation3.gif) |
(3) |
Therefore,
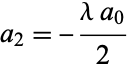 |
(4) |
and
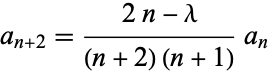 |
(5) |
for 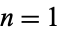 , 2, .... Since (4) is just a special case of (5),
, 2, .... Since (4) is just a special case of (5),
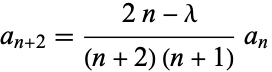 |
(6) |
for 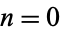 , 1, ....
, 1, ....
The linearly independent solutions are then
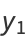 |
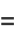 |
![a_0[1-lambda/(2!)x^2-((4-lambda)lambda)/(4!)x^4-((8-lambda)(4-lambda)lambda)/(6!)x^6-...]](http://mathworld.wolfram.com/images/equations/HermiteDifferentialEquation/Inline6.gif) |
(7) |
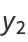 |
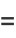 |
![a_1[x+((2-lambda))/(3!)x^3+((6-lambda)(2-lambda))/(5!)x^5+...].](http://mathworld.wolfram.com/images/equations/HermiteDifferentialEquation/Inline9.gif) |
(8) |
These can be done in closed form as
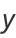 |
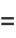 |
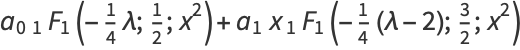 |
(9) |
 |
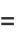 |
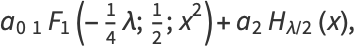 |
(10) |
where 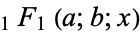 is a confluent hypergeometric function of the first kind and
is a confluent hypergeometric function of the first kind and 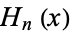 is a Hermite polynomial. In particular, for
is a Hermite polynomial. In particular, for 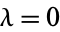 , 2, 4, ..., the solutions can be written
, 2, 4, ..., the solutions can be written
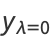 |
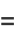 |
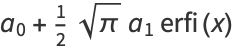 |
(11) |
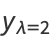 |
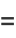 |
![a_0[e^(x^2)-sqrt(pi)xerfi(x)]+xa_1](http://mathworld.wolfram.com/images/equations/HermiteDifferentialEquation/Inline24.gif) |
(12) |
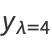 |
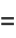 |
![1/4{2e^(x^2)xa_1-(2x^2-1)[4a_0+sqrt(pi)a_1erfi(x)]},](http://mathworld.wolfram.com/images/equations/HermiteDifferentialEquation/Inline27.gif) |
(13) |
where 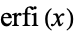 is the erfi function.
is the erfi function.
If 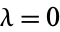 , then Hermite's differential equation becomes
, then Hermite's differential equation becomes
 |
(14) |
which is of the form  and so has solution
and so has solution
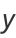 |
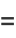 |
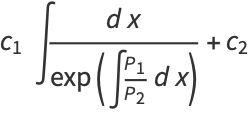 |
(15) |
 |
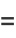 |
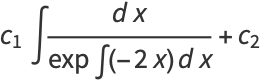 |
(16) |
 |
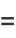 |
 |
(17) |



|
|
|
|
للعاملين في الليل.. حيلة صحية تجنبكم خطر هذا النوع من العمل
|
|
|
|
|
|
|
"ناسا" تحتفي برائد الفضاء السوفياتي يوري غاغارين
|
|
|
|
|
|
|
بمناسبة مرور 40 يومًا على رحيله الهيأة العليا لإحياء التراث تعقد ندوة ثقافية لاستذكار العلامة المحقق السيد محمد رضا الجلالي
|
|
|