Duffing Differential Equation

The most general forced form of the Duffing equation is

(1)

Depending on the parameters chosen, the equation can take a number of special forms. For example, with no damping and no forcing,  and taking the plus sign, the equation becomes

(2)

(Bender and Orszag 1978, p. 547; Zwillinger 1997, p. 122). This equation can display chaotic behavior. For , the equation represents a "hard spring," and for , it represents a "soft spring." If , the phase portrait curves are closed.

If instead we take , , reset the clock so that , and use the minus sign, the equation is then

(3)

This can be written as a system of first-order ordinary differential equations as

			(4)
			(5)

(Wiggins 1990, p. 5) which, in the unforced case, reduces to

			(6)
			(7)

(Wiggins 1990, p. 6; Ott 1993, p. 3).

The fixed points of this set of coupled differential equations are given by

(8)

so , and

			(9)
			(10)

giving . The fixed points are therefore , , and .

Analysis of the stability of the fixed points can be point by linearizing the equations. Differentiating gives

			(11)
			(12)
			(13)

which can be written as the matrix equation

(14)

Examining the stability of the point (0,0):

(15)

(16)

But , so  is real. Since , there will always be one positive root, so this fixed point is unstable. Now look at (, 0). The characteristic equation is

(17)

which has roots

(18)

For , , so the point is asymptotically stable. If , , so the point is linearly stable (Wiggins 1990, p. 10). However, if , the radical gives an imaginary part and the real part is , so the point is unstable. If , , which has a positive real root, so the point is unstable. If , then , so both roots are positive and the point is unstable.

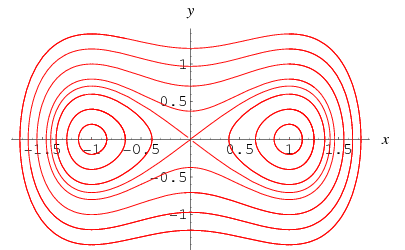
Interestingly, the special case  with no forcing,

			(19)
			(20)

can be integrated by quadratures. Differentiating (19) and plugging in (20) gives

(21)

Multiplying both sides by  gives

(22)

But this can be written

(23)

so we have an invariant of motion ,

(24)

Solving for  gives

(25)

(26)

so

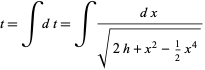(27)

(Wiggins 1990, p. 29).

Note that the invariant of motion  satisfies

(28)

(29)

so the equations of the Duffing oscillator are given by the Hamiltonian system

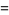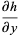			(30)
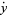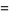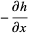			(31)

(Wiggins 1990, p. 31).

REFERENCES:

Bender, C. M. and Orszag, S. A. Advanced Mathematical Methods for Scientists and Engineers. New York: McGraw-Hill, p. 547, 1978.

Ott, E. Chaos in Dynamical Systems. New York: Cambridge University Press, 1993.

Tabor, M. Chaos and Integrability in Nonlinear Dynamics: An Introduction. New York: Wiley, p. 35, 1989.

Trott, M. "The Mathematica Guidebooks Additional Material: Wigner Function of a Duffing Oscillator." http://www.mathematicaguidebooks.org/additions.shtml#N_1_08.

Wiggins, S. "Application to the Dynamics of the Damped, Forced Duffing Oscillator." §1.2E in Introduction to Applied Nonlinear Dynamical Systems and Chaos. New York: Springer-Verlag, pp. 5-6, 10, 23, 26-32, 44-45, 50-51, and 153-175, 1990.

Zwillinger, D. (Ed.). CRC Standard Mathematical Tables and Formulae. Boca Raton, FL: CRC Press, p. 413, 1995.

Zwillinger, D. Handbook of Differential Equations, 3rd ed. Boston, MA: Academic Press, p. 122, 1997.