
آخر المواضيع المضافة


 تاريخ الرياضيات
تاريخ الرياضيات
 الرياضيات في الحضارات المختلفة
الرياضيات في الحضارات المختلفة 
 الرياضيات المتقطعة
الرياضيات المتقطعة
 الجبر
الجبر
 الهندسة
الهندسة 
 المعادلات التفاضلية و التكاملية
المعادلات التفاضلية و التكاملية 
 التحليل
التحليل
 علماء الرياضيات
علماء الرياضيات |
Read More
Date: 5-7-2018
Date: 26-12-2018
Date: 24-5-2018
|
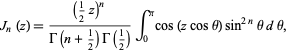 |
(1) |
where 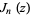 is a Bessel function of the first kind and
is a Bessel function of the first kind and 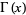 is a gamma function. It can be derived from Sonine's integral. With
is a gamma function. It can be derived from Sonine's integral. With 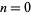 , the integral becomes Parseval's integral.
, the integral becomes Parseval's integral.
In complex analysis, let 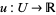 be a harmonic function on a neighborhood of the closed disk
be a harmonic function on a neighborhood of the closed disk 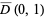 , then for any point
, then for any point 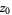 in the open disk
in the open disk 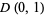 ,
,
 |
(2) |
In polar coordinates on 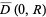 ,
,
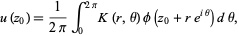 |
(3) |
where 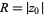 and
and 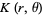 is the Poisson kernel. For a circle,
is the Poisson kernel. For a circle,
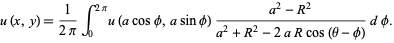 |
(4) |
For a sphere,
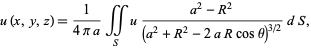 |
(5) |
where
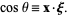 |
REFERENCES:
Krantz, S. G. "The Poisson Integral." §7.3.1 in Handbook of Complex Variables. Boston, MA: Birkhäuser, pp. 92-93, 1999.
Morse, P. M. and Feshbach, H. Methods of Theoretical Physics, Part I. New York: McGraw-Hill, pp. 373-374, 1953.



|
|
|
|
تفوقت في الاختبار على الجميع.. فاكهة "خارقة" في عالم التغذية
|
|
|
|
|
|
|
أمين عام أوبك: النفط الخام والغاز الطبيعي "هبة من الله"
|
|
|
|
|
|
|
بيان مكتب المرجع الديني الأعلى سماحة آية الله العظمى السيد علي الحسيني السيستاني (دام ظله) عقب الهجوم الإرهابي على المسافرين الأبرياء في مدينة پاراچنار، في پاكستان
|
|
|