Haversine
المؤلف:
Abramowitz, M. and Stegun, I. A.
المصدر:
Handbook of Mathematical Functions with Formulas, Graphs, and Mathematical Tables, 9th printing. New York: Dover,
الجزء والصفحة:
...
10-10-2019
1852
Haversine
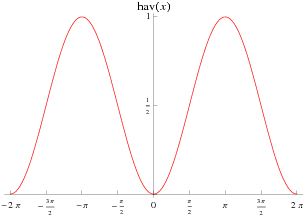
The haversine, also called the haversed sine, is a little-used entire trigonometric function defined by
where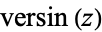 
is the versine, 
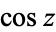is the cosine, and 
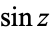is the sine.
The haversine is implemented in the Wolfram Language as Haversine[z].
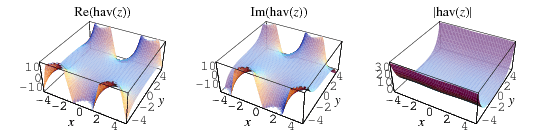
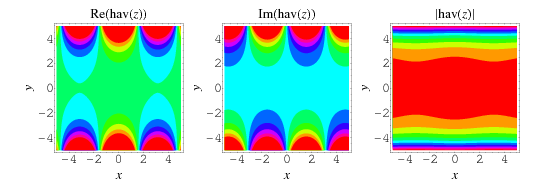
The haversine can be extended to the complex plane as illustrated above.
Its derivative is given by
 |
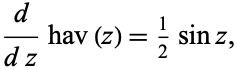(4)
|
and its indefinite integral by
 |
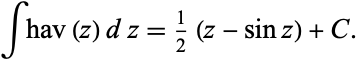(5)
|
It has Maclaurin series
REFERENCES:
Abramowitz, M. and Stegun, I. A. (Eds.). Handbook of Mathematical Functions with Formulas, Graphs, and Mathematical Tables, 9th printing. New York: Dover, p. 78, 1972.
Smart, W. M. Text-Book on Spherical Astronomy, 6th ed. Cambridge, England: Cambridge University Press, p. 18, 1960.
الاكثر قراءة في التفاضل و التكامل
اخر الاخبار
اخبار العتبة العباسية المقدسة
