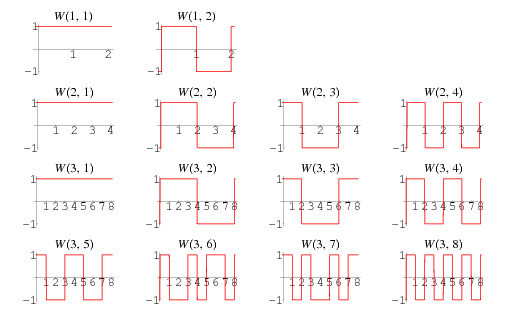
The Walsh functions consist of trains of square pulses (with the allowed states being 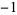 and 1) such that transitions may only occur at fixed intervals of a unit time step, the initial state is always 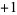, and the functions satisfy certain other orthogonality relations. In particular, the  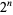Walsh functions of order  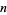are given by the rows of the Hadamard matrix  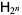when arranged in so-called "sequency" order (Thompson et al. 1986, p. 204; Wolfram 2002, p. 1073). There are  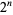Walsh functions of length 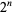, illustrated above for 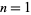, 2, and 3.

Walsh functions were used by electrical engineers such as Frank Fowle in the 1890s to find transpositions of wires that minimized crosstalk and were introduced into mathematics by Walsh (1923; Wolfram 2002, p. 1073).

Amazingly, concatenating the Walsh functions  (while simultaneously replacing 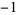s by 0s), where  is the ceiling function, gives the Thue-Morse sequence (Wolfram 2002, p. 1073). The values of  are given explicitly by 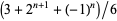, and the first few are 1, 2, 3, 6, 11, 22, 43, 86, 171, ... (OEIS A005578).

Walsh functions can be ordered in a number of ways, illustrated above (Wolfram 2002, p. 1073). The sequency 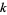 of a Walsh function is defined as half the number of zero crossings in one cycle of the time base. In sequency order (left figure), each row has one more color change than the preceding row. In natural (or Hadamard) order (middle figure), the Walsh functions display a nested structure. Dyadic (or Paley) order (right figure) is related to Gray code reordering of the rows (Wolfram 2002, p. 1073).

Walsh functions with nonidentical sequencies are orthogonal, as are the functions 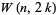 and 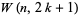. The product of two Walsh functions is also a Walsh function.

Harmuth (1969) designates the even Walsh functions 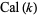 and the odd Walsh functions ,

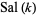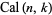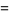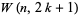			(1)
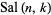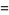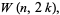			(2)

where 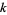 is the sequency.

Taking the matrix product of a set of two-dimensional data (represented as a square matrix with size a power of two) with a corresponding array of Walsh functions is known as the Walsh transform (Wolfram 2002, p. 1073). Walsh transforms can be performed particular efficiently, resulting in the so-called fast Walsh transform.

REFERENCES:

Beauchamp, K. G. Walsh Functions and Their Applications. London: Academic Press, 1975.

Harmuth, H. F. "Applications of Walsh Functions in Communications." IEEE Spectrum 6, 82-91, 1969.

Sloane, N. J. A. Sequence A005578/M0788 in "The On-Line Encyclopedia of Integer Sequences."

Thompson, A. R.; Moran, J. M.; and Swenson, G. W. Jr. Interferometry and Synthesis in Radio Astronomy. New York: Wiley, p. 204, 1986.

Tzafestas, S. G. Walsh Functions in Signal and Systems Analysis and Design. New York: Van Nostrand Reinhold, 1985.

Walsh, J. L. "A Closed Set of Normal Orthogonal Functions." Amer. J. Math. 45, 5-24, 1923.

Wolfram, S. A New Kind of Science. Champaign, IL: Wolfram Media, pp. 573 and 1072-1073, 2002.

اخر الاخبار

اخبار العتبة العباسية المقدسة

قسم صناعة الشبابيك يشرع بإدامة شباكين قديمين لمرقد الإمامين العسكريين (عليهما السلام)

فرقة العباس (عليه السلام) تختتم خدماتها المقدمة للزائرين في سامراء

موكب العتبتين المقدستين يحيي ذكرى استشهاد الإمام الهادي (عليه السلام) في سامراء

العتبة العسكرية المقدسة تكرّم وفد العتبة العباسية المقدسة لمشاركته في تقديم الخدمات للزائرين

المزيد

الآخبار الصحية

كنز غذائي على طبقك.. ماذا تفعل السبانخ بجسمك؟

ما لا يتوقعه أحد.. "سر غذائي" في الجبن الدسم

لتحسين الهضم والنوم.. هذا أفضل وقت لتناول العشاء

10 طرق بسيطة وغير مألوفة لحرق المزيد من السعرات يوميا

المزيد

الآخبار التكنلوجية

سابقة بعالم الطيران.. طائرة تقرر الهبوط بنفسها بعد ظرف طارئ

"الإنفلونزا الخارقة" تكتسح دول العالم.. وتثير قلقا كبيرا

مرحلة ما قبل الأعراض.. دواء جديد يستهدف "شرارة" الزهايمر

إزالة ثاني أكسيد الكربون من الغلاف الجوي.. ما دور المحيطات والبحار؟

المزيد