Condon-Shortley Phase
المؤلف:
Arfken, G.
المصدر:
Mathematical Methods for Physicists, 3rd ed. Orlando, FL: Academic Press
الجزء والصفحة:
...
23-9-2019
2151
Condon-Shortley Phase
The Condon-Shortley phase is the factor of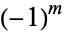 
that occurs in some definitions of the spherical harmonics (e.g., Arfken 1985, p. 682) to compensate for the lack of inclusion of this factor in the definition of the associated Legendre polynomials (e.g., Arfken 1985, p. 669).
Using the Condon-Shortley convention in the definition of the spherical harmonic after omitting it in the definition of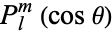 
gives
(Arfken 1985, p. 692), whereas using the definition of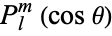 
that already includes it gives
(e.g., the Wolfram Language).
The Condon-Shortley phase is not necessary in the definition of the spherical harmonics, but including it simplifies the treatment of angular moment in quantum mechanics. In particular, they are a consequence of the ladder operators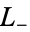 
and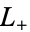 
(Arfken 1985, p. 693).
REFERENCES:
Arfken, G. Mathematical Methods for Physicists, 3rd ed. Orlando, FL: Academic Press, pp. 682 and 692, 1985.
Condon, E. U. and Shortley, G. The Theory of Atomic Spectra. Cambridge, England: Cambridge University Press, 1951.
Shore, B. W. and Menzel, D. H. Principles of Atomic Spectra. New York: Wiley, p. 158, 1968.
الاكثر قراءة في التفاضل و التكامل
اخر الاخبار
اخبار العتبة العباسية المقدسة
