Bernoulli Polynomial
المؤلف:
Abramowitz, M. and Stegun, I. A.
المصدر:
"Bernoulli and Euler Polynomials and the Euler-Maclaurin Formula." §23.1 in Handbook of Mathematical Functions with Formulas, Graphs, and Mathematical Tables, 9th printing. New York: Dover
الجزء والصفحة:
...
15-9-2019
2321
Bernoulli Polynomial
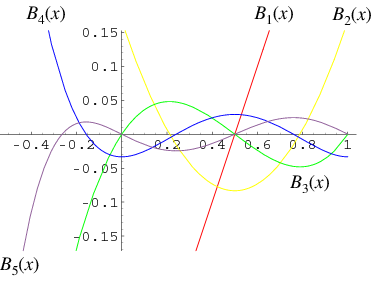
There are two definitions of Bernoulli polynomials in use. The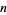 
th Bernoulli polynomial is denoted here by 
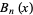(Abramowitz and Stegun 1972), and the archaic form of the Bernoulli polynomial by 
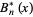(or sometimes 
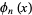). When evaluated at zero, these definitions correspond to the Bernoulli numbers,
The Bernoulli polynomials are an Appell sequence with
 |
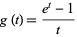(3)
|
(Roman 1984, p. 31), giving the generating function
 |
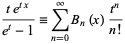(4)
|
(Abramowitz and Stegun 1972, p. 804), first obtained by Euler (1738). The first few Bernoulli polynomials are
Whittaker and Watson (1990, p. 126) define an older type of "Bernoulli polynomial" by writing
 |
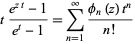(12)
|
instead of (12). This gives the polynomials
 |
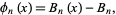(13)
|
where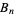 
is a Bernoulli number, the first few of which are
The Bernoulli polynomials also satisfy
 |
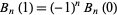(19)
|
and
 |
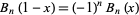(20)
|
(Lehmer 1988). For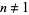 
,
 |
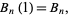(21)
|
so
 |
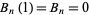(22)
|
for odd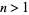 
.
They also satisfy the relation
 |
(23)
|
(Whittaker and Watson 1990, p. 127).
For rational values of 
, 
can be expressed for positive integers 
in terms of Bernoulli and Euler numbers, for example
Bernoulli (1713) defined the polynomials in terms of sums of the powers of consecutive integers,
![sum_(k=0)^(m-1)k^(n-1)=1/n[B_n(m)-B_n(0)].](http://mathworld.wolfram.com/images/equations/BernoulliPolynomial/NumberedEquation10.gif) |
(29)
|
The Bernoulli polynomials satisfy the recurrence relation
 |
(30)
|
(Appell 1882), and obey the identity
 |
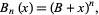(31)
|
where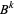 
is interpreted as the Bernoulli number 
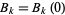. Another related identity is
 |
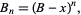(32)
|
where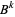 
is interpreted as the Bernoulli polynomial 
.
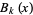Hurwitz gave the Fourier series
 |
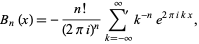(33)
|
for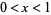 
, where the prime in the summation indicates that the term 
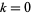is omitted. Performing the sum gives
 |
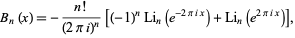(34)
|
where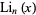 
is the polylogarithm function. Raabe (1851) found
 |
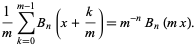(35)
|
A sum identity involving the Bernoulli polynomials is
 |
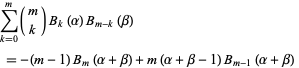(36)
|
for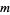 
an integer. A sum identity due to S. M. Ruiz is
 |
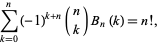(37)
|
where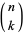 
is a binomial coefficient. The Bernoulli polynomials are also given by the formula
 |
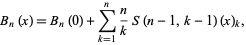(38)
|
where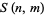 
is a Stirling number of the second kind and 
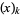is a falling factorial (Roman 1984, p. 94). A general identity is given by
 |
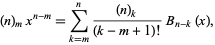(39)
|
which simplifies to
 |
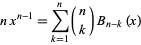(40)
|
(Roman 1984, p. 97). Gosper gave the identity
 |
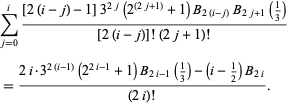(41)
|
A generalization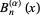 
of the Bernoulli polynomials with an additional free parameter can be defined such that 
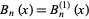(Roman 1984, p. 93). These polynomials have the generating function
 |
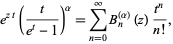(42)
|
and are implemented in the Wolfram Language as NorlundB[n, alpha, z].
REFERENCES:
Abramowitz, M. and Stegun, I. A. (Eds.). "Bernoulli and Euler Polynomials and the Euler-Maclaurin Formula." §23.1 in Handbook of Mathematical Functions with Formulas, Graphs, and Mathematical Tables, 9th printing. New York: Dover, pp. 804-806, 1972.
Appell, P. E. "Sur une classe de polynomes." Annales d'École Normal Superieur, Ser. 2 9, 119-144, 1882.
Arfken, G. Mathematical Methods for Physicists, 3rd ed. Orlando, FL: Academic Press, p. 330, 1985.
Bernoulli, J. Ars conjectandi. Basel, Switzerland, p. 97, 1713. Published posthumously.
Euler, L. "Methodus generalis summandi progressiones." Comment. Acad. Sci. Petropol. 6, 68-97, 1738.
Lehmer, D. H. "A New Approach to Bernoulli Polynomials." Amer. Math. Monthly. 95, 905-911, 1988.
Lucas, E. Ch. 14 in Théorie des Nombres. Paris, 1891.
Prudnikov, A. P.; Marichev, O. I.; and Brychkov, Yu. A. "The Generalized Zeta Function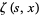 
, Bernoulli Polynomials 
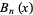, Euler Polynomials 
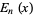, and Polylogarithms 
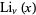." §1.2 in Integrals and Series, Vol. 3: More Special Functions. Newark, NJ: Gordon and Breach, pp. 23-24, 1990.
Raabe, J. L. "Zurückführung einiger Summen und bestimmten Integrale auf die Jakob Bernoullische Function." J. reine angew. Math. 42, 348-376, 1851.
Roman, S. "The Bernoulli Polynomials." §4.2.2 in The Umbral Calculus. New York: Academic Press, pp. 93-100, 1984.
Spanier, J. and Oldham, K. B. "The Bernoulli Polynomial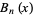 
." Ch. 19 in An Atlas of Functions. Washington, DC: Hemisphere, pp. 167-173, 1987.
Whittaker, E. T. and Watson, G. N. A Course in Modern Analysis, 4th ed. Cambridge, England: Cambridge University Press, 1990.
الاكثر قراءة في التفاضل و التكامل
اخر الاخبار
اخبار العتبة العباسية المقدسة
