The prime zeta function

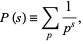(1)

where the sum is taken over primes is a generalization of the Riemann zeta function

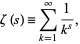(2)

where the sum is over all positive integers. In other words, the prime zeta function 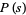 is the Dirichlet generating function of the characteristic function of the primes 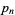.  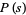is illustrated above on positive the real axis, where the imaginary part is indicated in yellow and the real part in red. (The sign difference in the imaginary part compared to the plot appearing in Fröberg is presumably a result of the use of a different convention for .)

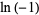Various terms and notations are used for this function. The term "prime zeta function" and notation 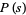 were used by Fröberg (1968), whereas Cohen (2000) uses the notation .

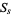The series converges absolutely for 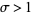, where 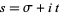, can be analytically continued to the strip  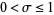(Fröberg 1968), but not beyond the line  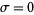(Landau and Walfisz 1920, Fröberg 1968) due to the clustering of singular points along the imaginary axis arising from the nontrivial zeros of the Riemann zeta function on the critical line .

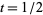As illustrated in the left figure above (where the real part is indicated in red and the imaginary part in yellow), the function has singular points along the real axis for 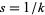 where 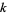 runs through all positive integers without a square factor. For  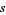close to 1,  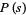has the expansion

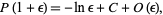(3)

where 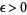 and

			(4)
			(5)

(OEIS A143524), where 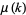 is the Möbius function and  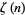is the Riemann zeta function (Fröberg 1968).

The prime zeta function is plotted above for  and  (Fröberg 1968).

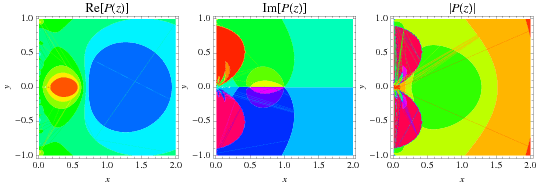
The prime zeta function is illustrated above in the complex plane.

The prime zeta function can be expressed in terms of the Riemann zeta function by

			(6)
			(7)
			(8)
			(9)

Inverting then gives

(10)

(Glaisher 1891, Fröberg 1968, Cohen 2000).

The prime zeta function is implemented in the Wolfram Language as PrimeZetaP[s].

The Dirichlet generating function of the composite numbers 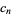 is given by

			(11)
			(12)

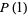, The analog of the harmonic series, diverges, but convergence of the series for  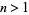is quadratic. However, dropping the initial term from the sum for  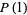(and adding the Euler-Mascheroni constant  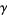to the result) gives simply the Mertens constant

			(13)
			(14)

(OEIS A077761).

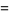Artin's constant  is connected with  by

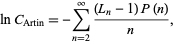(15)

where 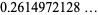 is a Lucas number (Ribenboim 1998, Gourdon and Sebah).

The values of 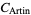 for the first few integers  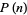starting with two are given in the following table. Merrifield (1881) computed  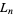for 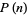 up to 35 to 15 digits, and Liénard (1948) computed  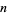up to 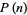 to 50 digits (Ribenboim 1996). Gourdon and Sebah give values to 60 digits for .

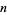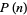	OEIS
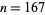2	A085548	0.452247
3	A085541	0.174763
4	A085964	0.0769931
5	A085965	0.035755
6	A085966	0.0170701
7	A085967	0.00828383
8	A085968	0.00406141
9	A085969	0.00200447
10		0.000993604

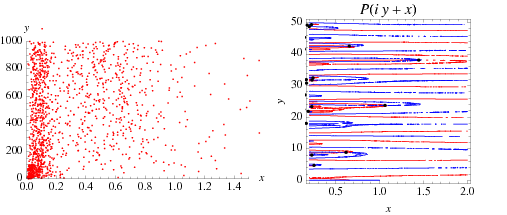
According to Fröberg (1968), very little is known about the roots 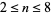. The plots above show the positions of zeros (left figure) and contours of zero real (red) and imaginary (blue) parts in a portion of the complex plane, with roots indicated as black dots (right figure).

REFERENCES:

Cohen, H. "High Precision Computation of Hardy-Littlewood Constants." Preprint. http://www.math.u-bordeaux.fr/~cohen/hardylw.dvi.

Cohen, H. Advanced Topics in Computational Number Theory. New York: Springer-Verlag, 2000.

Dahlquist, G. "On the Analytic Continuation of Eulerian Products." Arkiv för Math. 1, 533-554, 1951.

Davis, H. T. Tables of the Higher Mathematical Functions, Vol. 2. Bloomington, IN: Principia Press, p. 249, 1933.

Fröberg, C.-E. "On the Prime Zeta Function." BIT 8, 187-202, 1968.

Glaisher, J. W. L. "On the Sums of Inverse Powers of the Prime Numbers." Quart. J. Math. 25, 347-362, 1891.

Gourdon, X. and Sebah, P. "Some Constants from Number Theory." http://numbers.computation.free.fr/Constants/Miscellaneous/constantsNumTheory.html.

Hardy, G. H. and Wright, E. M. An Introduction to the Theory of Numbers, 5th ed. Oxford, England: Oxford University Press, pp. 355-356, 1979.

Haselgrove, C. B. and Miller, J. C. P. "Tables of the Riemann Zeta Function." Royal Society Mathematical Tables, Vol. 6. Cambridge, England: Cambridge University Press, p. 58, 1960.

Landau, E. and Walfisz, A. "Über die Nichfortsetzbarkeit einiger durch Dirichletsche Reihen definierter Funktionen." Rend. Circ. Math. Palermo 44, 82-86, 1920.

Liénard, R. Tables fondamentales à 50 décimales des sommes 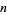, , 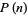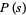. Paris: Centre de Docum. Univ., 1948.

Merrifield, C. W. "The Sums of the Series of Reciprocals of the Prime Numbers and of Their Powers." Proc. Roy. Soc. London 33, 4-10, 1881.

Muñoz García, E. and Pérez Marco, R. "The Product Over All Primes is 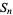." Preprint IHES/M/03/34. May 2003. http://inc.web.ihes.fr/prepub/PREPRINTS/M03/Resu/resu-M03-34.html.

Muñoz García, E. and Pérez Marco, R. "The Product Over All Primes is 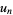." Commun. Math. Phys. 277, 69-81, 2008.

Ribenboim, P. The New Book of Prime Number Records. New York: Springer-Verlag, 1996.

Sloane, N. J. A. Sequences A077761, A085541, A085548, A085964, A085965, A085966, A085967, A085968, A085969, and A143524 in "The On-Line Encyclopedia of Integer Sequences."