Li,s Criterion
المؤلف:
Bombieri, E. and Lagarias, J. C
المصدر:
"Complements to Li,s Criterion for the Riemann Hypothesis." J. Number Th. 77
الجزء والصفحة:
...
9-9-2019
2686
Li's Criterion
Li's criterion states that the Riemann hypothesis is equivalent to the statement that, for
 |
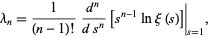(1)
|
where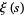 
is the xi-function, 
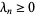for every positive integer 
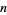(Li 1997). Li's constants can be written in alternate form as
 |
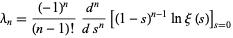(2)
|
(Coffey 2004).
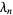can also be written as a sum of nontrivial zeros 
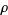of 
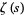as
 |
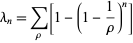(3)
|
(Li 1997, Coffey 2004).
A recurrence for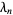 
in terms of 
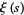is given by
 |
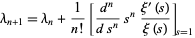(4)
|
(Coffey 2004).
The first few explicit values of the constantes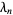 
are
where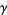 
is the Euler-Mascheroni constant and 
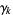are Stieltjes constants. 
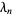can be computed efficiently in closed form using recurrence formulas due to Coffey (2004), namely
 |
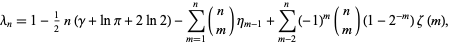(8)
|
where
 |
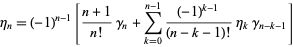(9)
|
and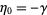 
.
 |
 |
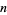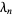OEIS |
| 1 |
0.0230957... |
A074760 |
| 2 |
0.0923457... |
A104539 |
| 3 |
0.2076389... |
A104540 |
| 4 |
0.3687904... |
A104541 |
| 6 |
0.5755427... |
A104542 |
| 7 |
1.1244601... |
A306340 |
| 8 |
1.4657556... |
A306341 |
Edwards 2001 (p. 160) gave a numerical value for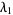 
, and numerical values to six digits up to 
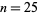were tabulated by Coffey (2004).
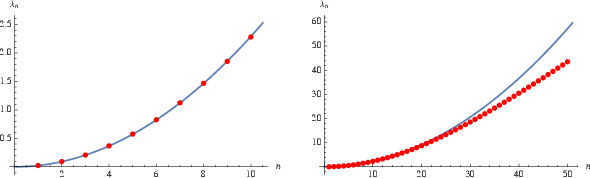
While the values of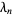 
up to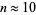 
are remarkably well fit by a parabola with
 |
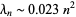(10)
|
(left figure above), larger terms show clear variation from a parabolic fit (right figure).
REFERENCES:
Bombieri, E. and Lagarias, J. C. "Complements to Li's Criterion for the Riemann Hypothesis." J. Number Th. 77, 274-287, 1999.
Coffey, M. W. "Relations and Positivity Results for Derivatives of the Riemann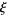 
Function." J. Comput. Appl. Math. 166, 525-534, 2004.
Edwards, H. M. Riemann's Zeta Function. New York: Dover, 2001.
Keiper, J. B. "Power Series Expansions of Riemann's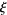 
Function." Math. Comput. 58, 765-773, 1992.
Li, X.-J. "The Positivity of a Sequence of Numbers and the Riemann Hypothesis." J. Number Th. 65, 325-333, 1997.
Sloane, N. J. A. Sequences A074760, A104539, A104540, A104541, and A104542 in "The On-Line Encyclopedia of Integer Sequences."
الاكثر قراءة في التفاضل و التكامل
اخر الاخبار
اخبار العتبة العباسية المقدسة
