Nested Radical
Expressions of the form
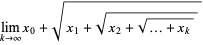 |
(1)
|
are called nested radicals. Herschfeld (1935) proved that a nested radical of real nonnegative terms converges iff 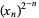 is bounded. He also extended this result to arbitrary powers (which include continued square roots and continued fractions as well), a result is known as Herschfeld's convergence theorem.
is bounded. He also extended this result to arbitrary powers (which include continued square roots and continued fractions as well), a result is known as Herschfeld's convergence theorem.
Nested radicals appear in the computation of pi,
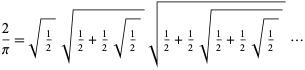 |
(2)
|
(Vieta 1593; Wells 1986, p. 50; Beckmann 1989, p. 95), in trigonometrical values of cosine and sine for arguments of the form 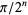 , e.g.,
, e.g.,
Nest radicals also appear in the computation of the golden ratio
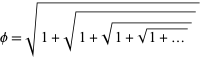 |
(7)
|
and plastic constant
![P=RadicalBox[<span style=]() {1, +, RadicalBox[{1, +, RadicalBox[{1, +, ...}, 3]}, 3]}, 3]. " src="http://mathworld.wolfram.com/images/equations/NestedRadical/NumberedEquation4.gif" style="height:44px; width:164px" /> {1, +, RadicalBox[{1, +, RadicalBox[{1, +, ...}, 3]}, 3]}, 3]. " src="http://mathworld.wolfram.com/images/equations/NestedRadical/NumberedEquation4.gif" style="height:44px; width:164px" /> |
(8)
|
Both of these are special cases of
![x=RadicalBox[<span style=]() {a, +, RadicalBox[{a, +, ...}, n]}, n], " src="http://mathworld.wolfram.com/images/equations/NestedRadical/NumberedEquation5.gif" style="height:26px; width:120px" /> {a, +, RadicalBox[{a, +, ...}, n]}, n], " src="http://mathworld.wolfram.com/images/equations/NestedRadical/NumberedEquation5.gif" style="height:26px; width:120px" /> |
(9)
|
which can be exponentiated to give
![x^n=a+RadicalBox[<span style=]() {a, +, RadicalBox[{a, +, ...}, n]}, n], " src="http://mathworld.wolfram.com/images/equations/NestedRadical/NumberedEquation6.gif" style="height:26px; width:148px" /> {a, +, RadicalBox[{a, +, ...}, n]}, n], " src="http://mathworld.wolfram.com/images/equations/NestedRadical/NumberedEquation6.gif" style="height:26px; width:148px" /> |
(10)
|
so solutions are
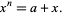 |
(11)
|
In particular, for 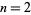 , this gives
, this gives
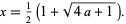 |
(12)
|
The silver constant is related to the nested radical expression
![RadicalBox[<span style=]() {7, +, 7, RadicalBox[{7, +, ...}, 3]}, 3]. " src="http://mathworld.wolfram.com/images/equations/NestedRadical/NumberedEquation9.gif" style="height:26px; width:106px" /> {7, +, 7, RadicalBox[{7, +, ...}, 3]}, 3]. " src="http://mathworld.wolfram.com/images/equations/NestedRadical/NumberedEquation9.gif" style="height:26px; width:106px" /> |
(13)
|
There are a number of general formula for nested radicals (Wong and McGuffin). For example,
![x=RadicalBox[<span style=]() {{(, {1, -, q}, )}, {x, ^, n}, +, q, {x, ^, {(, {n, -, 1}, )}}, RadicalBox[{{(, {1, -, q}, )}, {x, ^, n}, +, q, {x, ^, {(, {n, -, 1}, )}}, RadicalBox[..., n]}, n]}, n] " src="http://mathworld.wolfram.com/images/equations/NestedRadical/NumberedEquation10.gif" style="height:44px; width:302px" /> {{(, {1, -, q}, )}, {x, ^, n}, +, q, {x, ^, {(, {n, -, 1}, )}}, RadicalBox[{{(, {1, -, q}, )}, {x, ^, n}, +, q, {x, ^, {(, {n, -, 1}, )}}, RadicalBox[..., n]}, n]}, n] " src="http://mathworld.wolfram.com/images/equations/NestedRadical/NumberedEquation10.gif" style="height:44px; width:302px" /> |
(14)
|
which gives as special cases
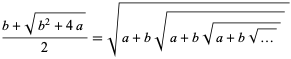 |
(15)
|
(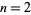 ,
, 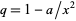 ,
, 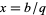 ),
),
![x=RadicalBox[<span style=]() {{x, ^, {(, {n, -, 1}, )}}, RadicalBox[{{x, ^, {(, {n, -, 1}, )}}, RadicalBox[{{x, ^, {(, {n, -, 1}, )}}, RadicalBox[..., n]}, n]}, n]}, n] " src="http://mathworld.wolfram.com/images/equations/NestedRadical/NumberedEquation12.gif" style="height:59px; width:193px" /> {{x, ^, {(, {n, -, 1}, )}}, RadicalBox[{{x, ^, {(, {n, -, 1}, )}}, RadicalBox[{{x, ^, {(, {n, -, 1}, )}}, RadicalBox[..., n]}, n]}, n]}, n] " src="http://mathworld.wolfram.com/images/equations/NestedRadical/NumberedEquation12.gif" style="height:59px; width:193px" /> |
(16)
|
(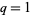 ), and
), and
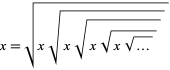 |
(17)
|
(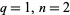 ). Equation (14) also gives rise to
). Equation (14) also gives rise to
![q^((n^k-1)/(n-1))x^(n^j)=RadicalBox[<span style=]() {{q, ^, {(, {{(, {{n, ^, {(, {k, +, 1}, )}}, -, n}, )}, /, {(, {n, -, 1}, )}}, )}}, {(, {1, -, q}, )}, {x, ^, {(, {n, ^, {(, {j, +, 1}, )}}, )}}, +, ...}, n]
...+RadicalBox[{{q, ^, {(, {{(, {{n, ^, {(, {k, +, 2}, )}}, -, n}, )}, /, {(, {n, -, 1}, )}}, )}}, {(, {1, -, q}, )}, {x, ^, {(, {n, ^, {(, {j, +, 2}, )}}, )}}, +, RadicalBox[..., n]}, n]^_, " src="http://mathworld.wolfram.com/images/equations/NestedRadical/NumberedEquation14.gif" style="height:101px; width:299px" /> {{q, ^, {(, {{(, {{n, ^, {(, {k, +, 1}, )}}, -, n}, )}, /, {(, {n, -, 1}, )}}, )}}, {(, {1, -, q}, )}, {x, ^, {(, {n, ^, {(, {j, +, 1}, )}}, )}}, +, ...}, n]
...+RadicalBox[{{q, ^, {(, {{(, {{n, ^, {(, {k, +, 2}, )}}, -, n}, )}, /, {(, {n, -, 1}, )}}, )}}, {(, {1, -, q}, )}, {x, ^, {(, {n, ^, {(, {j, +, 2}, )}}, )}}, +, RadicalBox[..., n]}, n]^_, " src="http://mathworld.wolfram.com/images/equations/NestedRadical/NumberedEquation14.gif" style="height:101px; width:299px" /> |
(18)
|
which gives the special case for 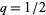 ,
, 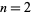 ,
, 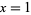 , and
, and 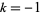 ,
,
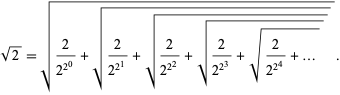 |
(19)
|
Equation (◇) can be generalized to
![x^(1/(n-1))=RadicalBox[<span style=]() {x, RadicalBox[{x, RadicalBox[{x, ...}, n]}, n]}, n] " src="http://mathworld.wolfram.com/images/equations/NestedRadical/NumberedEquation16.gif" style="height:44px; width:153px" /> {x, RadicalBox[{x, RadicalBox[{x, ...}, n]}, n]}, n] " src="http://mathworld.wolfram.com/images/equations/NestedRadical/NumberedEquation16.gif" style="height:44px; width:153px" /> |
(20)
|
for integers 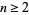 , which follows from
, which follows from
In particular, taking 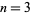 gives
gives
![sqrt(x)=RadicalBox[<span style=]() {x, RadicalBox[{x, RadicalBox[{x, ...}, 3]}, 3]}, 3]. " src="http://mathworld.wolfram.com/images/equations/NestedRadical/NumberedEquation17.gif" style="height:44px; width:142px" /> {x, RadicalBox[{x, RadicalBox[{x, ...}, 3]}, 3]}, 3]. " src="http://mathworld.wolfram.com/images/equations/NestedRadical/NumberedEquation17.gif" style="height:44px; width:142px" /> |
(26)
|
(J. R. Fielding, pers. comm., Oct. 8, 2002).
Ramanujan discovered
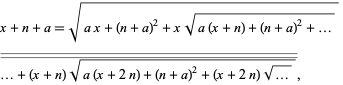 |
(27)
|
which gives the special cases
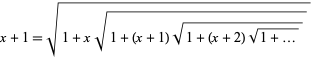 |
(28)
|
for 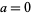 ,
, 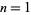 (Ramanujan 1911; Ramanujan 2000, p. 323; Pickover 2002, p. 310), and
(Ramanujan 1911; Ramanujan 2000, p. 323; Pickover 2002, p. 310), and
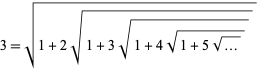 |
(29)
|
for 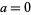 ,
, 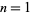 , and
, and 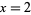 . The justification of this process in general (and in the particular example of
. The justification of this process in general (and in the particular example of 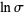 , where
, where 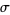 is Somos's quadratic recurrence constant) is given by Vijayaraghavan (in Ramanujan 2000, p. 348).
is Somos's quadratic recurrence constant) is given by Vijayaraghavan (in Ramanujan 2000, p. 348).
An amusing nested radical follows rewriting the series for e
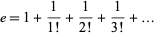 |
(30)
|
as
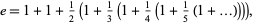 |
(31)
|
so
![x^(e-2)=sqrt(xRadicalBox[<span style=]() {x, RadicalBox[{x, RadicalBox[{x, ...}, 5]}, 4]}, 3]) " src="http://mathworld.wolfram.com/images/equations/NestedRadical/NumberedEquation23.gif" style="height:59px; width:168px" /> {x, RadicalBox[{x, RadicalBox[{x, ...}, 5]}, 4]}, 3]) " src="http://mathworld.wolfram.com/images/equations/NestedRadical/NumberedEquation23.gif" style="height:59px; width:168px" /> |
(32)
|
(J. R. Fielding, pers. comm., May 15, 2002).
REFERENCES:
Beckmann, P. A History of Pi, 3rd ed. New York: Dorset Press, 1989.
Berndt, B. C. Ramanujan's Notebooks, Part IV. New York: Springer-Verlag, pp. 14-20, 1994.
Borwein, J. M. and de Barra, G. "Nested Radicals." Amer. Math. Monthly 98, 735-739, 1991.
Herschfeld, A. "On Infinite Radicals." Amer. Math. Monthly 42, 419-429, 1935.
Jeffrey, D. J. and Rich, A. D. In Computer Algebra Systems (Ed. M. J. Wester). Chichester, England: Wiley, 1999.
Landau, S. "A Note on 'Zippel Denesting.' " J. Symb. Comput. 13, 31-45, 1992a.
Landau, S. "Simplification of Nested Radicals." SIAM J. Comput. 21, 85-110, 1992b.
Landau, S. "How to Tangle with a Nested Radical." Math. Intell. 16, 49-55, 1994.
Landau, S. "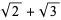 : Four Different Views." Math. Intell. 20, 55-60, 1998.
: Four Different Views." Math. Intell. 20, 55-60, 1998.
Pólya, G. and Szegö, G. Problems and Theorems in Analysis, Vol. 1. New York: Springer-Verlag, 1997.
Ramanujan, S. Question No. 298. J. Indian Math. Soc. 1911.
Ramanujan, S. Collected Papers of Srinivasa Ramanujan (Ed. G. H. Hardy, P. V. S. Aiyar, and B. M. Wilson). Providence, RI: Amer. Math. Soc., p. 327, 2000.
Sizer, W. S. "Continued Roots." Math. Mag. 59, 23-27, 1986.
Vieta, F. Uriorum de rebus mathematicis responsorum. Liber VII. 1593. Reprinted in New York: Georg Olms, pp. 398-400 and 436-446, 1970.
Wells, D. The Penguin Dictionary of Curious and Interesting Numbers. Middlesex, England: Penguin Books, 1986.
Wong, B. and McGuffin, M. "The Museum of Infinite Nested Radicals." http://www.dgp.toronto.edu/~mjmcguff/math/nestedRadicals.html.
 الاكثر قراءة في التفاضل و التكامل
الاكثر قراءة في التفاضل و التكامل
 اخر الاخبار
اخر الاخبار
اخبار العتبة العباسية المقدسة


