Min Max

The common logarithm is the logarithm to base 10. The notation 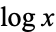 is used by physicists, engineers, and calculator keypads to denote the common logarithm. However, mathematicians generally use the same symbol to mean the natural logarithm ln, 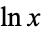. Worse still, in Russian literature the notation  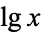is used to denote a base-10 logarithm, which conflicts with the use of the symbol lg to indicate the logarithm to base 2. To avoid all ambiguity, it is best to explicitly specify  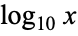when the logarithm to base 10 is intended. In this work, 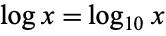,  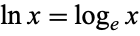is used for the natural logarithm, and  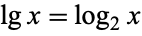is used for the logarithm to the base 2.

The situation is complicated even more by the fact that number theorists (e.g., Ivić 2003) commonly use the notation 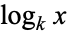 to denote the nested natural logarithm .

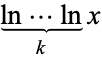The common logarithm is implemented in the Wolfram Language as Log[10, x] and Log10[x].

Hardy and Wright (1979, p. 8) assert that the common logarithm has "no mathematical interest."

Common and natural logarithms can be expressed in terms of each other as

and

Min   Max       Re       Im

The common logarithm extended into the complex plane is illustrated above.

REFERENCES:

Hardy, G. H. and Wright, E. M. An Introduction to the Theory of Numbers, 5th ed. Oxford, England: Clarendon Press, 1979.

Ivić, A. "On a Problem of Erdős Involving the Largest Prime Factor of 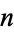." 5 Nov 2003. http://arxiv.org/abs/math.NT/0311056.