Saalschütz,s Theorem
المؤلف:
Hardy, G. H.
المصدر:
Ramanujan: Twelve Lectures on Subjects Suggested by His Life and Work, 3rd ed. New York: Chelsea,
الجزء والصفحة:
...
18-6-2019
2237
Saalschütz's Theorem
![_3F_2[-x,-y,-z; n+1,-x-y-z]=(Gamma(n+1)Gamma(x+y+n+1))/(Gamma(x+n+1)Gamma(y+n+1))
×(Gamma(y+z+n+1)Gamma(z+x+n+1))/(Gamma(z+n+1)Gamma(x+y+z+n+1)),](http://mathworld.wolfram.com/images/equations/SaalschuetzsTheorem/NumberedEquation1.gif) |
(1)
|
where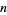 
is a generalized hypergeometric function and 
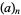is the gamma function. It can be derived from the Dougall-Ramanujan identity and written in the symmetric form
 |
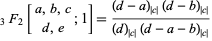(2)
|
for
 |
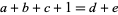(3)
|
with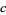 
a nonpositive integer and 
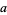the Pochhammer symbol (Bailey 1935, p. 9; Petkovšek et al. 1996; Koepf 1998, p. 32). If one of 
, 
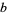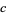, and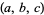 
is nonpositive but it is not known which, an alternative formulation due to W. Gosper (pers. comm.) gives the form
 |
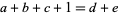(4)
|
which is symmetric in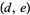 
and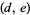 
.
If instead
 |
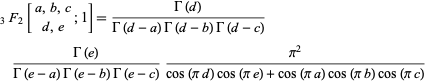(5)
|
then
 |
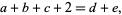(6)
|
(W. Gosper, pers. comm.).
REFERENCES:
Bailey, W. N. "Saalschütz's Theorem." §2.2 in Generalised Hypergeometric Series. Cambridge, England: Cambridge University Press, p. 9, 1935.
Dougall, J. "On Vandermonde's Theorem and Some More General Expansions." Proc. Edinburgh Math. Soc. 25, 114-132, 1907.
Hardy, G. H. Ramanujan: Twelve Lectures on Subjects Suggested by His Life and Work, 3rd ed. New York: Chelsea, p. 104, 1999.
Koepf, W. Hypergeometric Summation: An Algorithmic Approach to Summation and Special Function Identities. Braunschweig, Germany: Vieweg, 1998.
Petkovšek, M.; Wilf, H. S.; and Zeilberger, D. A=B. Wellesley, MA: A K Peters, pp. 43 and 126, 1996. http://www.cis.upenn.edu/~wilf/AeqB.html.
Saalschütz, L. "Eine Summationsformel." Z. für Math. u. Phys. 35, 186-188, 1890.
Saalschütz, L. "Über einen Spezialfall der hypergeometrischen Reihe dritter Ordnung." Z. für Math. u. Phys. 36, 278-295 and 321-327, 1891.
Shepard, W. F. "Summation of the Coefficients of Some Terminating Hypergeometric Series." Proc. London Math. Soc. 10, 469-478, 1912.
الاكثر قراءة في التفاضل و التكامل
اخر الاخبار
اخبار العتبة العباسية المقدسة
