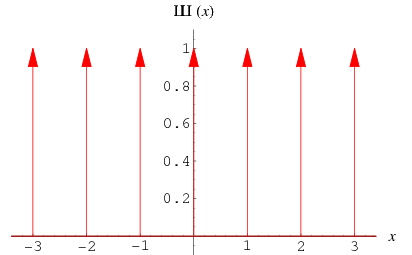
The shah function is defined by

			(1)
			(2)

where 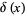 is the delta function, so  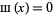for 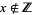 (i.e.,  is not an integer). The shah function is also called the sampling symbol or replicating symbol (Bracewell 1999, p. 77), and is implemented in the Wolfram Language as DiracComb[x].

It obeys the identities

			(3)
			(4)
			(5)
			(6)

The shah function is normalized so that

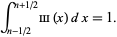(7)

The "sampling property" is

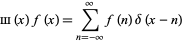(8)

and the "replicating property" is

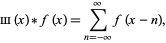(9)

where 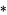 denotes convolution.

The two-dimensional sampling function, sometimes called the bed-of-nails function, is given by

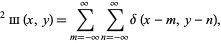(10)

which can be adjusted using a series of weights as

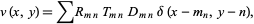(11)

where 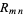 is a reliability weight,  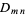is a density weight (weighting function), and  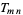is a taper. The two-dimensional shah function satisfies

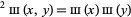(12)

(Bracewell 1999, p. 85).

REFERENCES:

Bracewell, R. "The Sampling or Replicating Symbol 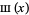." In The Fourier Transform and Its Applications, 3rd ed. New York: McGraw-Hill, pp. 77-79 and 85, 1999.