The class of all regular sequences of particularly well-behaved functions equivalent to a given regular sequence. A distribution is sometimes also called a "generalized function" or "ideal function." As its name implies, a generalized function is a generalization of the concept of a function. For example, in physics, a baseball being hit by a bat encounters a force from the bat, as a function of time. Since the transfer of momentum from the bat is modeled as taking place at an instant, the force is not actually a function. Instead, it is a multiple of the delta function. The set of distributions contains functions (locally integrable) and Radon measures. Note that the term "distribution" is closely related to statistical distributions.

Generalized functions are defined as continuous linear functionals over a space of infinitely differentiable functions such that all continuous functions have derivatives which are themselves generalized functions. The most commonly encountered generalized function is the delta function. Vladimirov (1971) contains a nice treatment of distributions from a physicist's point of view, while the multivolume work by Gel'fand and Shilov (1964abcde) is a classic and rigorous treatment of the field. A result of Schwarz shows that distributions can't be consistently defined over the complex numbers .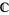

While it is possible to add distributions, it is not possible to multiply distributions when they have coinciding singular support. Despite this, it is possible to take the derivative of a distribution, to get another distribution. Consequently, they may satisfy a linear partial differential equation, in which case the distribution is called a weak solution. For example, given any locally integrable function 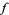 it makes sense to ask for solutions  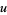of Poisson's equation

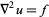(1)

by only requiring the equation to hold in the sense of distributions, that is, both sides are the same distribution. The definitions of the derivatives of a distribution 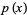 are given by

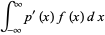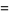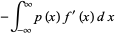			(2)
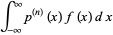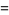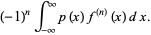			(3)

Distributions also differ from functions because they are covariant, that is, they push forward. Given a smooth function 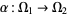, a distributi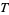on  on 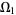 pushes forward to a distribution on 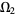. In contrast, a real functi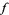on  on 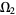 pulls back to a function on 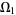, namely .

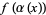Distributions are, by definition, the dual to the smooth functions of compact support, with a particular topology. For example, the delta function 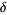 is the linear functional 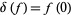. The distribution corresponding to a function  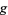is

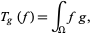(4)

and the distribution corresponding to a measure 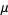 is

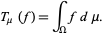(5)

The pushforward map of a distribution 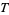 along 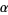 is defined by

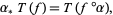(6)

and the derivative of 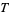 is defined by  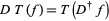where 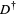 is the formal adjoint of 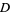. For example, the first derivative of the delta function is given by

(7)

As is the case for any function space, the topology determines which linear functionals are continuous, that is, are in the dual vector space. The topology is defined by the family of seminorms,

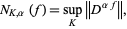(8)

where sup denotes the supremum. It agrees with the C-infty topology on compact subsets. In this topology, a sequence converges, 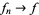, iff there is a compact set  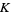such that all  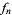are supported in  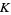and every derivative 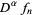converges uniformly to  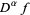in 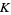. Therefore, the constant function 1 is a distribution, because if  then

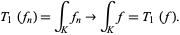(9)

REFERENCES:

Brychkov, Yu. A. and Prudnikov, A. P. Integral Transforms of Generalized Functions. New York: Gordon and Breach, 1989.

Gel'fand, I. M. and Shilov, G. E. Generalized Functions, Vol. 1: Properties and Operations. New York: Academic Press, 1964a.

Gel'fand, I. M. and Shilov, G. E. Generalized Functions, Vol. 2: Spaces of Fundamental and Generalized Functions. New York: Academic Press, 1964b.

Gel'fand, I. M. and Shilov, G. E. Generalized Functions, Vol. 3: Theory of Differential Equations. New York: Academic Press, 1964c.

Gel'fand, I. M. and Shilov, G. E. Generalized Functions, Vol. 4: Applications of Harmonic Analysis. New York: Academic Press, 1964d.

Gel'fand, I. M. and Shilov, G. E. Generalized Functions, Vol. 5: Integral Geometry and Representation Theory. New York: Academic Press, 1964e.

Kanwal, R. P. Generalized Functions: Theory and Technique, 2nd ed. Boston, MA: Birkhäuser, 1998.

Vladimirov, V. S. Equations of Mathematical Physics. New York: Dekker, 1971.

اخر الاخبار

اخبار العتبة العباسية المقدسة

فرقة العباس تنظم مجلس عزائها السنوي بذكرى شهادة النبي (صلى الله عليه وآله) في النجف

قسم الشؤون الفكرية وجامعة الكوفة يعقدان شراكة علمية لتدريب الطلبة على صيانة المخطوطات وحفظها

بالتزامن مع ذكرى شهادته.. قسم الشؤون الفكرية يصدر كتابًا عن النبي الأعظم (صلى الله عليه وآله)

بالصور.. جموع المؤمنين تحيي ذكرى شهادة الرسول الأكرم عند مرقد الإمام علي (صلوات الله عليهما)

المزيد

الآخبار الصحية

لون أسنانك يتحدث عن صحتك.. إليك ما يقول

عادة يومية بسيطة تخفض الكوليسترول وتحمي القلب

الزنجبيل.. دواء سحري لحماية القلب

المشروبات شديدة السخونة.. "خطر خفي" يهدد صحتك

المزيد

الآخبار التكنلوجية

كيف يمكن لعادات القيادة السيئة أن تؤثر على قيمة سيارتك

في طوفان الذكاء الاصطناعي.. نصائح لحجز "تذكرة النجاة"

هكذا يسرق "قراصنة الذكاء الاصطناعي" المليارات بطرق بسيطة

فيديو لانفجار كرة نارية في سماء اليابان.. ما تفسير ذلك؟

المزيد