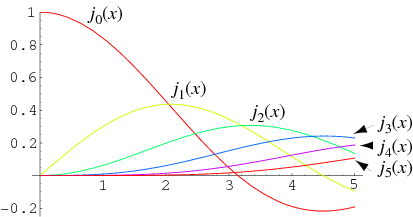
The spherical Bessel function of the first kind, denoted 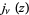, is defined by

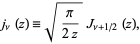(1)

where 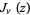 is a Bessel function of the first kind and, in general,  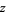and  are complex numbers.

The function is most commonly encountered in the case 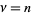 an integer, in which case it is given by

			(2)
			(3)
			(4)

Equation (4) shows the close connection between 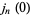 and the sinc function .

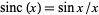Spherical Bessel functions 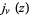 are implemented in the Wolfram Language as SphericalBesselJ[nu, z] using the definition

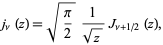(5)

which differs from the "traditional version" along the branch cut of the square root function, i.e., the negative real axis (e.g., at 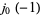), but has nicer analytic properties for complex  (Falloon 2001).

The first few functions are

			(6)
			(7)
			(8)

which includes the special value

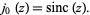(9)

REFERENCES:

Abramowitz, M. and Stegun, I. A. (Eds.). "Spherical Bessel Functions." §10.1 in Handbook of Mathematical Functions with Formulas, Graphs, and Mathematical Tables, 9th printing. New York: Dover, pp. 437-442, 1972.

Arfken, G. "Spherical Bessel Functions." §11.7 in Mathematical Methods for Physicists, 3rd ed. Orlando, FL: Academic Press, pp. 622-636, 1985.

Falloon, P. E. Theory and Computation of Spheroidal Harmonics with General Arguments. Masters thesis. Perth, Australia: University of Western Australia, 2001. http://www.physics.uwa.edu.au/pub/Theses/2002/Falloon/Masters_Thesis.pdf.