Hankel Function of the Second Kind
المؤلف:
Arfken, G
المصدر:
"Hankel Functions." §11.4 in Mathematical Methods for Physicists, 3rd ed. Orlando, FL: Academic Press
الجزء والصفحة:
...
24-3-2019
2376
Hankel Function of the Second Kind
 |
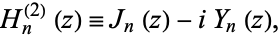(1)
|
where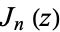 
is a Bessel function of the first kind and 
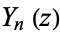is a Bessel function of the second kind. Hankel functions of the second kind is implemented in the Wolfram Language as HankelH2[n, z].
Hankel functions of the second kind can be represented as a contour integral using
![H_n^((2))(z)=1/(ipi)int_(-infty [lower half plane])^0(e^((z/2)(t-1/t)))/(t^(n+1))dt.](http://mathworld.wolfram.com/images/equations/HankelFunctionoftheSecondKind/NumberedEquation2.gif) |
(2)
|
The derivative of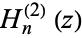 
is given by
![d/(dz)H_n^((2))(z)=1/2[H_(n-1)^((2))(z)-H_(n+1)^((2))(z)].](http://mathworld.wolfram.com/images/equations/HankelFunctionoftheSecondKind/NumberedEquation3.gif) |
(3)
|
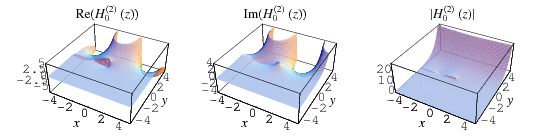
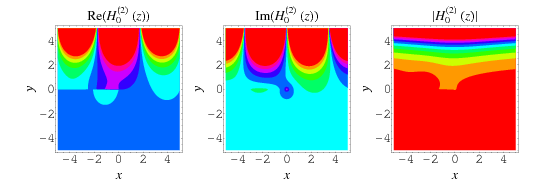
The plots above show the structure of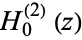 
in the complex plane.
REFERENCES:
Arfken, G. "Hankel Functions." §11.4 in Mathematical Methods for Physicists, 3rd ed. Orlando, FL: Academic Press, pp. 604-610, 1985.
Morse, P. M. and Feshbach, H. Methods of Theoretical Physics, Part I. New York: McGraw-Hill, pp. 623-624, 1953.
الاكثر قراءة في التفاضل و التكامل
اخر الاخبار
اخبار العتبة العباسية المقدسة
