Second Derivative Test
المؤلف:
Abramowitz, M. and Stegun, I. A.
المصدر:
Handbook of Mathematical Functions with Formulas, Graphs, and Mathematical Tables, 9th printing. New York: Dover
الجزء والصفحة:
...
24-9-2018
2282
Second Derivative Test
Suppose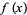 
is a function of 
that is twice differentiable at a stationary point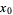 
.
1. If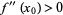 
, then 
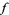has a local minimum at 
.
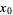2. If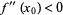 
, then 
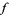has a local maximum at 
.
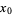The extremum test gives slightly more general conditions under which a function with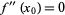 
is a maximum or minimum.
If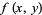 
is a two-dimensional function that has a local extremum at a point 
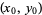and has continuous partial derivatives at this point, then 
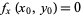and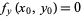 
. The second partial derivatives test classifies the point as a local maximum or local minimum.
Define the second derivative test discriminant as
Then
1. If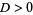 
and 
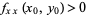, the point is a local minimum.
2. If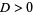 
and 
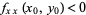, the point is a local maximum.
3. If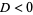 
, the point is a saddle point.
4. If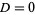 
, higher order tests must be used.
REFERENCES:
Abramowitz, M. and Stegun, I. A. (Eds.). Handbook of Mathematical Functions with Formulas, Graphs, and Mathematical Tables, 9th printing. New York: Dover, p. 14, 1972.
Thomas, G. B. Jr. and Finney, R. L. "Maxima, Minima, and Saddle Points." §12.8 in Calculus and Analytic Geometry, 8th ed. Reading, MA: Addison-Wesley, pp. 881-891, 1992.
الاكثر قراءة في التفاضل و التكامل
اخر الاخبار
اخبار العتبة العباسية المقدسة
