


 الفيزياء الكلاسيكية
الفيزياء الكلاسيكية
 الكهربائية والمغناطيسية
الكهربائية والمغناطيسية
 علم البصريات
علم البصريات
 الفيزياء الحديثة
الفيزياء الحديثة
 النظرية النسبية
النظرية النسبية
 الفيزياء النووية
الفيزياء النووية
 فيزياء الحالة الصلبة
فيزياء الحالة الصلبة
 الليزر
الليزر
 علم الفلك
علم الفلك
 المجموعة الشمسية
المجموعة الشمسية
 الطاقة البديلة
الطاقة البديلة
 الفيزياء والعلوم الأخرى
الفيزياء والعلوم الأخرى
 مواضيع عامة في الفيزياء
مواضيع عامة في الفيزياء|
Read More
Date: 29-12-2020
Date: 24-5-2016
Date: 29-10-2020
|
The vector product
We have discovered how to construct a scalar from the components of two general vectors a and b. Can we also construct a vector which is not just a linear combination of a and b? Consider the following definition:
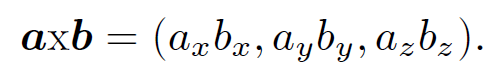 (1.1)
(1.1)
Is axb a proper vector? Suppose that a = (1, 0, 0), b = (0, 1, 0). Clearly, axb = 0. However, if we rotate the basis through 45± about the z-axis then 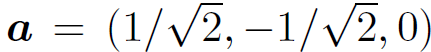 ,
, 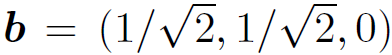 , and axb = (1/2,-1/2, 0). Thus, axb does not transform like a vector because its magnitude depends on the choice of axis. So, above definition is a bad one. Consider, now, the cross product or vector product:
, and axb = (1/2,-1/2, 0). Thus, axb does not transform like a vector because its magnitude depends on the choice of axis. So, above definition is a bad one. Consider, now, the cross product or vector product:
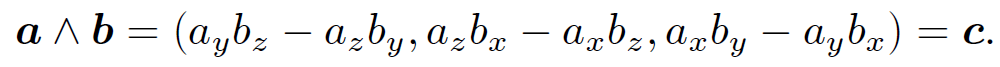 (1.2)
(1.2)
Does this rather unlikely combination transform like a vector? Let us try rotating the basis through θ degrees about the z-axis using. In the new basis
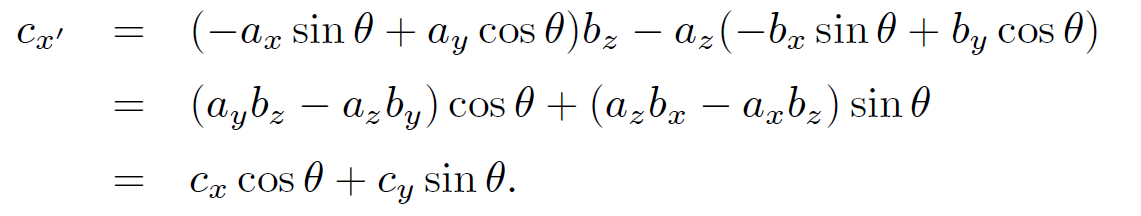 (1.3)
(1.3)
Thus, the x-component of a˄b transforms correctly. It can easily be shown that the other components transform correctly as well. Thus, a˄b is a proper vector. The cross product is anticommutative:
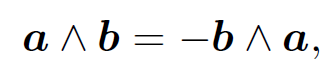 (1.4)
(1.4)
distributive:
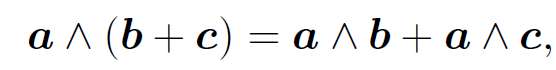 (1.5)
(1.5)
but is not associative:
 (1.6)
(1.6)
The cross product transforms like a vector, which means that it must have a well defined direction and magnitude. We can show that a ˄ b is perpendicular to both a and b. Consider a . a ˄ b. If this is zero then the cross product must be perpendicular to a. Now
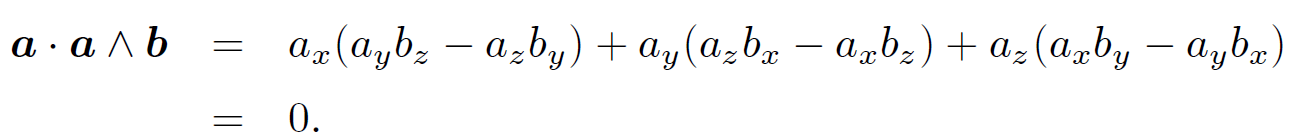 (1.7)
(1.7)
Therefore, a ^ b is perpendicular to a. Likewise, it can be demonstrated that a ˄ b is perpendicular to b. The vectors a, b, and a ˄b form a right-handed set like the unit vectors i, j, and k: i ˄ j = k. This defines a unique direction for a ˄ b, which is obtained from the right-hand rule. Let us now evaluate the magnitude of a ˄ b. We have
 (1.8)
(1.8)
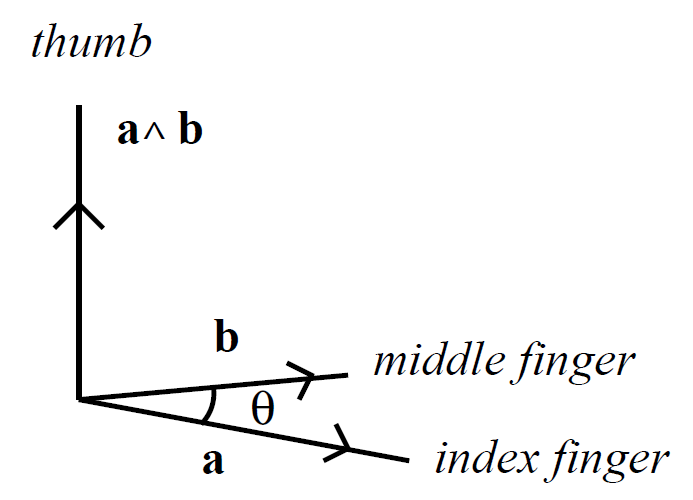
Thus,
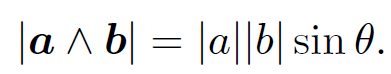 (1.9)
(1.9)
Clearly, a ˄ a = 0 for any vector, since θ is always zero in this case. Also, if a ˄ b = 0 then either |a| = 0, |b| = 0, or b is parallel (or antiparallel) to a. Consider the parallelogram defined by vectors a and b. The scalar area is ab sin θ. The vector area has the magnitude of the scalar area and is normal to the plane of the parallelogram, which means that it is perpendicular to both a and b. Clearly, the vector area is given by
 (1.10)
(1.10)
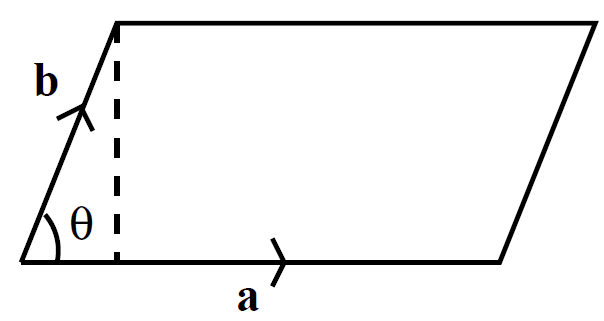
with the sense obtained from the right-hand grip rule by rotating a on to b. Suppose that a force F is applied at position r. The moment about the origin O is the product of the magnitude of the force and the length of the lever arm OQ. Thus, the magnitude of the moment is |F||r| sin θ. The direction of a moment is conventionally the direction of the axis through O about which the force tries
to rotate objects, in the sense determined by the right-hand grip rule. It follows that the vector moment is given by
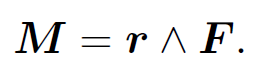 (1.11)
(1.11)



|
|
|
|
4 أسباب تجعلك تضيف الزنجبيل إلى طعامك.. تعرف عليها
|
|
|
|
|
|
|
أكبر محطة للطاقة الكهرومائية في بريطانيا تستعد للانطلاق
|
|
|
|
|
|
|
العتبة العباسية المقدسة تبحث مع العتبة الحسينية المقدسة التنسيق المشترك لإقامة حفل تخرج طلبة الجامعات
|
|
|