Definition : A topological space X is said to be simply-connected if it is path connected, and any continuous map f: ∂D → X mapping the boundary circle ∂D of a closed disc D into X can be extended continuously over the whole of the disk.

Example Rⁿ is simply-connected for all n. Indeed any continuous map f: ∂D → Rⁿ defined over the boundary ∂D of the closed unit disk D can be extended to a continuous map F: D → Rⁿ over the whole disk by setting F(rx) = rf(x) for all x ∈ ∂D and r ∈ [0, 1].

let E be a topological space that is homeomorphic to the closed disk D,  and let ∂E = h(∂D), where ∂D is the boundary circle of the disk D and h: D → E is a homeomorphism from D to E. Then any continuous map g: ∂E→X mapping ∂E into a simply-connected space X extends continuously to the whole of E. Indeed there exists a continuous map F: D → X which extends g ◦ h: ∂D → X, and the map F ◦ h⁻¹ : E → X then extends the map g.

Theorem 1.3 A path-connected topological space X is simply-connected if and only if π₁(X, x) is trivial for all x ∈ X.

Proof Suppose that the space X is simply-connected. Let γ: [0, 1] → X be a loop based at some point x of X. Now the unit square is homeomorphic to the unit disk, and therefore any continuous map defined over the boundary of the square can be continuously extended over the whole of the square. It follows that there exists a continuous map F: [0, 1] × [0, 1] → X such that F(t, 0) = γ(t) and F(t, 1) = x for all t ∈ [0, 1], and F(0, τ ) = F(1, τ ) = x for all τ ∈ [0, 1]. Thus γ ≃ εx rel{0, 1}, where εx is the constant loop at x, and hence [γ] = [εx] in π1(X, x). This shows that π1(X, x) is trivial.

Conversely suppose that X is path-connected and π1(X, x) is trivial for all x ∈ X. Let f: ∂D → X be a continuous function defined on the boundary circle ∂D of the closed unit disk D in R² . We must show that f can be extended continuously over the whole of D. Let x = f(1, 0). There exists a continuous map G: [0, 1]×[0, 1] → X such that                                               G(t, 0) = f(cos(2πt),sin(2πt))  and G(t, 1) = x for all t ∈ [0, 1] and G(0, τ ) = G(1, τ ) = x for all τ ∈ [0, 1],  since π₁(X, x) is trivial. Moreover G(t₁, τ₁) = G(t₂, τ₂) whenever                                   q(t₁, τ₁) = q(t₂, τ₂), where

                        q(t, τ ) = ((1 − τ ) cos(2πt) + τ,(1 − τ ) sin(2πt))

for all t, τ ∈ [0, 1]. It follows that there is a well-defined function F: D → X such that F ◦ q = G. However q: [0, 1] × [0, 1] → D is a continuous surjection from a compact space to a Hausdorff space and is therefore an identification map. It follows that F:D → X is continuous (since a basic property of identification maps ensures that a function F: D → X is continuous if and only if F ◦ q: [0, 1] × [0, 1] → X is continuous). Moreover F: D → X extends the map f. We conclude that the space X is simply-connected, as required.

One can show that, if two points x1 and x2 in a topological space X can be joined by a path in X then π₁(X, x₁) and π₁(X, x₂) are isomorphic.

On combining this result with Theorem 1.3, we see that a path-connected topological space X is simply-connected if and only if π₁(X, x) is trivial for some x ∈ X.

Theorem 1.4 Let X be a topological space, and let U and V be open subsets of X, with U ∪V = X. Suppose that U and V are simply-connected, and that U ∩ V is non-empty and path-connected. Then X is itself simply-connected.

Proof We must show that any continuous function f: ∂D → X defined on the unit circle ∂D can be extended continuously over the closed unit disk D.

Now the preimages f⁻¹ (U) and f⁻¹ (V ) of U and V are open in ∂D (sincef is continuous), and ∂D = f⁻¹ (U) ∪ f⁻¹ (V ). It follows from the Lebesgue Lemma that there exists some      δ > 0 such that any arc in ∂D whose length is less than δ is entirely contained in one or other of the sets f⁻¹ (U) and f⁻¹ (V ). Choose points z₁, z₂, . . . , z_n around ∂D such that the distance from z_i to z_i+1 is less than δ for i = 1, 2, . . . , n−1 and the distance from z_n to z₁ is also less than δ. Then, for each i, the short arc joining z_i−1 to z_i is mapped by f into one or other of the open sets U and V .

Let x₀ be some point of U ⋂V . Now the sets U, V and U ⋂V are all pathconnected. Therefore we can choose paths α_i: [0, 1] → X for i = 1, 2, . . . , n such that α_i(0) = x₀, α_i(1) = f(z_i), α_i([0, 1]) ⊂ U whenever f(z_i) ∈ U, and α_i([0, 1]) ⊂ V whenever f(z_i) ∈ V . For convenience let α₀ = α_n Now, for each i, consider the sector Ti of the closed unit disk bounded by the line segments joining the centre of the disk to the points z_i−1 and z_i and by the short arc joining z_i−1 to z_i . Now this sector is homeomorphic to the closed unit disk, and therefore any continuous function mapping the boundary ∂T_i of T_i into a simply-connected space can be extended continuously over the whole of T_i . In particular, let F_i be the function on ∂Ti defined by

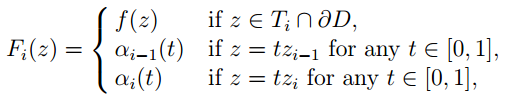
Note that Fi(∂T_i) ⊂ U whenever the short arc joining z_i−1 to z_i is mapped by f into U, and F_i(∂T_i) ⊂ V whenever this short arc is mapped into V . But U and V are both simply-connected. It follows that each of the functions F_i can be extended continuously over the whole of the sector T_i . Moreover the functions defined in this fashion on each of the sectors Ti agree with one another wherever the sectors intersect, and can therefore be pieced together to yield a continuous map defined over the the whole of the closed disk D which extends the map f, as required.

Example The n-dimensional sphere Sⁿ is simply-connected for all n > 1,  where S n = {x ∈ Rⁿ⁺¹ : |x| = 1}. Indeed let U = {x ∈ Sⁿ: x_n+1 > −1/2} and V = {x ∈ Sⁿ: x_n+1 <1/2}. Then U and V are homeomorphic to an n-dimensional ball, and are therefore simply-connected. Moreover U ∩ V is path-connected, provided that n > 1. It follows that Sⁿ is simply-connected for all n > 1.