
تاريخ الفيزياء

علماء الفيزياء


الفيزياء الكلاسيكية

الميكانيك

الديناميكا الحرارية


الكهربائية والمغناطيسية

الكهربائية

المغناطيسية

الكهرومغناطيسية


علم البصريات

تاريخ علم البصريات

الضوء

مواضيع عامة في علم البصريات

الصوت


الفيزياء الحديثة


النظرية النسبية

النظرية النسبية الخاصة

النظرية النسبية العامة

مواضيع عامة في النظرية النسبية

ميكانيكا الكم

الفيزياء الذرية

الفيزياء الجزيئية


الفيزياء النووية

مواضيع عامة في الفيزياء النووية

النشاط الاشعاعي


فيزياء الحالة الصلبة

الموصلات

أشباه الموصلات

العوازل

مواضيع عامة في الفيزياء الصلبة

فيزياء الجوامد


الليزر

أنواع الليزر

بعض تطبيقات الليزر

مواضيع عامة في الليزر


علم الفلك

تاريخ وعلماء علم الفلك

الثقوب السوداء


المجموعة الشمسية

الشمس

كوكب عطارد

كوكب الزهرة

كوكب الأرض

كوكب المريخ

كوكب المشتري

كوكب زحل

كوكب أورانوس

كوكب نبتون

كوكب بلوتو

القمر

كواكب ومواضيع اخرى

مواضيع عامة في علم الفلك

النجوم

البلازما

الألكترونيات

خواص المادة


الطاقة البديلة

الطاقة الشمسية

مواضيع عامة في الطاقة البديلة

المد والجزر

فيزياء الجسيمات


الفيزياء والعلوم الأخرى

الفيزياء الكيميائية

الفيزياء الرياضية

الفيزياء الحيوية

الفيزياء العامة


مواضيع عامة في الفيزياء

تجارب فيزيائية

مصطلحات وتعاريف فيزيائية

وحدات القياس الفيزيائية

طرائف الفيزياء

مواضيع اخرى
The displacement current
المؤلف:
Richard Fitzpatrick
المصدر:
Classical Electromagnetism
الجزء والصفحة:
p 108
3-1-2017
2478
The displacement current
Michael Faraday revolutionized physics in 1830 by showing that electricity and magnetism were interrelated phenomena. He achieved this breakthrough by careful experimentation. Between 1864 and 1873 James Clerk Maxwell achieved a similar breakthrough by pure thought. Of course, this was only possible because he was able to take the experimental results of Faraday, Ampere, etc., as his starting point. Prior to 1864 the laws of electromagnetism were written in integral form. Thus, Gauss's law was (in S.I. units) the flux of the electric field through closed surface equals the total enclosed charge divided by  The no magnetic monopole law was the flux of the magnetic field through any closed surface is zero. Faraday's law was the electromotive force generated around a closed loop equals minus the rate of change of the magnetic flux through the loop. Finally, Ampere's law was the line integral of the magnetic field around a closed loop equals the total current flowing through the loop times μ0. Maxwell's first great achievement was to realize that these laws could be expressed as a set of partial differential equations. Of course, he wrote his equations out in component form because modern vector notation did not come into vogue until about the time of the First World War. In modern notation, Maxwell first wrote
The no magnetic monopole law was the flux of the magnetic field through any closed surface is zero. Faraday's law was the electromotive force generated around a closed loop equals minus the rate of change of the magnetic flux through the loop. Finally, Ampere's law was the line integral of the magnetic field around a closed loop equals the total current flowing through the loop times μ0. Maxwell's first great achievement was to realize that these laws could be expressed as a set of partial differential equations. Of course, he wrote his equations out in component form because modern vector notation did not come into vogue until about the time of the First World War. In modern notation, Maxwell first wrote
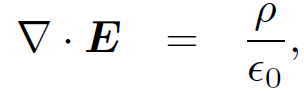 (1.1a)
(1.1a)
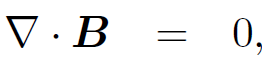 (1.1b)
(1.1b)
 (1.1c)
(1.1c)
 (1.1d)
(1.1d)
Maxwell's second great achievement was to realize that these equations are wrong. We can see that there is something slightly unusual about Eqs. (1.1). They are very unfair to electric fields! After all, time varying magnetic fields can induce electric fields, but electric fields apparently cannot affect magnetic fields in any way. However, there is a far more serious problem associated with the above equations, which we alluded to earlier on. Consider the integral form of the last Maxwell equation (i.e., Ampere's law)
 (1.2)
(1.2)
This says that the line integral of the magnetic field around a closed loop C is equal to μ0 times the flux of the current density through the loop. The problem is that the flux of the current density through a loop is not, in general, a well defined quantity. In order for the flux to be well defined the integral of j . dS over some surface S attached to a loop C must depend on C but not on the details of S. This is only the case if
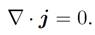 (1.3)
(1.3)
Unfortunately, the above condition is only satisfied for non-time varying fields. Why do we say that, in general, ∇ . j ≠ 0? Well, consider the flux of j over some closed surface S enclosing a volume V . This is clearly equivalent to the rate at which charge flows through S. However, if charge is a conserved quantity (and we certainly believe that it is) then the rate at which charge flows through S must equal the rate of decrease of the charge contained in volume V . Thus,
 (1.4)
(1.4)
Making use of Gauss' theorem, this yields
 (1.5)
(1.5)
Thus, ∇ . j = 0 is only true in a steady state (i.e., when ∂/∂t ≡ 0). The problem with Ampere's law is well illustrated by the following very famous example. Consider a long straight wire interrupted by a parallel plate capacitor. Suppose that C is some loop which circles the wire. In the non-time dependent situation the capacitor acts like a break in the wire, so no current flows, and no magnetic field is generated. There is clearly no problem with Ampere's law in this case. In the time dependent situation a transient current flows in the wire as the capacitor charges up, or charges down, so a transient magnetic field is generated. Thus, the line integral of the magnetic field around C is (transiently) non-zero. According to Ampere's law, the flux of the current through any surface attached to C should also be (transiently) non-zero. Let us consider two such surfaces. The first surface, S1, intersects the wire. This surface causes us no problem since the flux of j though the surface is clearly non-zero (because it intersects a current carrying wire). The second surface, S2, passes between the plates of the capacitor and, therefore, does not intersect the wire at all. Clearly, the flux of the current through this surface is zero. The current fluxes through surfaces S1 and S2 are obviously different. However, both surfaces are attached to the same loop C, so the fluxes should be the same according to Ampere's law. It would appear that Ampere's law is about to disintegrate! However, we notice that although the surface S2 does not intersect any electric current it does pass through a region of strong changing electric field as it threads between the plates of the charging (or discharging) capacitor. Perhaps, if we add a term involving ∂E/∂t to the right-hand side of Eq. (1.1d) we can somehow fix up Ampere's law? This is, essentially, how Maxwell reasoned more than one hundred years ago. Let us try out this scheme. Suppose that we write
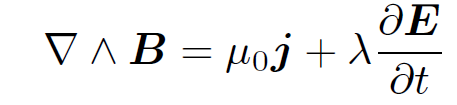 (1.6)
(1.6)
instead of Eq. (1.1d). Here, ¸ is some constant. Does this resolve our problem? We want the flux of the right-hand side of the above equation through some loop C to be well defined; i.e., it should only depend on C and not the particular surface S (which spans C) upon which it is evaluated. This is another way of saying that we want the divergence of the right-hand side to be zero. In fact, we can see that this is necessary for self consistency since the divergence of the left-hand side is automatically zero. So, taking the divergence of Eq. (1.6) we obtain
 (1.7)
(1.7)
But, we know that
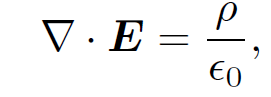 (1.8)
(1.8)
so combining the previous two equations we arrive at
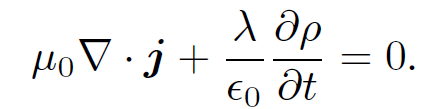 (1.9)
(1.9)
Now, our charge conservation law (1.5) can be written
 (1.10)
(1.10)
The previous two equations are in agreement provided λ =  μ0. So, if we modify the final Maxwell equation such that it reads
μ0. So, if we modify the final Maxwell equation such that it reads
 (1.11)
(1.11)
then we find that the divergence of the right-hand side is zero as a consequence of charge conservation. The extra term is called the ''displacement current" (this name was invented by Maxwell). In summary, we have shown that although the flux of the real current through a loop is not well defined, if we form the sum of the real current and the displacement current then the flux of this new quantity through a loop is well defined. Of course, the displacement current is not a current at all. It is, in fact, associated with the generation of magnetic fields by time varying electric fields. Maxwell came up with this rather curious name because many of his ideas regarding electric and magnetic fields were completely wrong. For instance, Maxwell believed in the ether, and he thought that electric and magnetic fields were some sort of stresses in this medium. He also thought that the displacement current was associated with displacements of the ether (hence, the name). The reason that these misconceptions did not invalidate his equations is quite simple. Maxwell based his equations on the results of experiments, and he added in his extra term so as to make these equations mathematically self consistent. Both of these steps are valid irrespective of the existence or non-existence of the ether. ''But, hang on a minute," you might say'', you can't go around adding terms to laws of physics just because you feel like it! The field equations (1.1) are derived directly from the results of famous nineteenth century experiments. If there is a new term involving the time derivative of the electric field which needs to be added into these equations, how come there is no corresponding nineteenth century experiment which demonstrates this? We have Ampere's law which shows that changing magnetic fields generate electric fields. Why is there no ''Joe Blogg's" law that says that changing electric fields generate magnetic fields?" This is a perfectly reasonable question. The answer is that the new term describes an effect which is far too small to have been observed in nineteenth century experiments. Let us demonstrate this. First, we shall show that it is comparatively easy to detect the induction of an electric field by a changing magnetic field in a desktop laboratory experiment. The Earth's magnetic field is about 1 gauss (that is, 10-4 tesla). Magnetic fields generated by electromagnets (which will fit on a laboratory desktop) are typically about one hundred times bigger that this. Let us, therefore, consider a hypothetical experiment in which a 100 gauss magnetic field is switched on suddenly. Suppose that the field ramps up in one tenth of a second. What electromotive force is generated in a 10 centimeter square loop of wire located in this field? Ampere's law is written
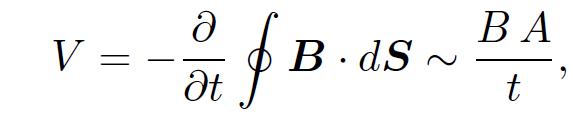 (1.12)
(1.12)
where B = 0.01 tesla is the field strength, A = 0.01 m2 is the area of the loop, and t = 0.1 seconds is the ramp time. It follows that V ~ 1 millivolt. Well, one millivolt is easily detectable. In fact, most hand-held laboratory voltmeters are calibrated in millivolts. It is clear that we would have no difficulty whatsoever detecting the magnetic induction of electric fields in a nineteenth century style laboratory experiment. Let us now consider the electric induction of magnetic fields. Suppose that our electric field is generated by a parallel plate capacitor of spacing one centimeter which is charged up to 100 volts. This gives a field of 104 volts per meter. Suppose, further, that the capacitor is discharged in one tenth of a second. The law of electric induction is obtained by integrating Eq. (1.11) and neglecting the first term on the right-hand side. Thus,
 (1.13)
(1.13)
Let us consider a loop 10 centimeters square. What is the magnetic field generated around this loop (we could try to measure this with a Hall probe). Very approximately we find that
 (1.14)
(1.14)
where l = 0.1 meters is the dimensions of the loop, B is the magnetic field strength, E = 104 volts per meter is the electric field, and t = 0.1 seconds is the decay time of the field. We find that B ~ 10-9 gauss. Modern technology is unable to detect such a small magnetic field, so we cannot really blame Faraday for not noticing electric induction in 1830. ''So", you might say'', why did you bother mentioning this displacement cur- rent thing in the first place if it is undetectable?" Again, a perfectly fair question. The answer is that the displacement current is detectable in some experiments. Suppose that we take an FM radio signal, amplify it so that its peak voltage is one hundred volts, and then apply it to the parallel plate capacitor in the previous hypothetical experiment. What size of magnetic field would this generate? Well, a typical FM signal oscillates at 109 Hz, so t in the previous example changes from 0.1 seconds to 10-9 seconds. Thus, the induced magnetic field is about10-1 gauss. This is certainly detectable by modern technology. So, it would seem that if the electric field is oscillating fast then electric induction of magnetic fields is an observable effect. In fact, there is a virtually infallible rule for deciding whether or not the displacement current can be neglected in Eq. (1.11). If electromagnetic radiation is important then the displacement current must be included. On the other hand, if electromagnetic radiation is unimportant then the displacement current can be safely neglected. Clearly, Maxwell's inclusion of the displacement current in Eq. (1.11) was a vital step in his later realization that his equations allowed propagating wave-like solutions. These solutions are, of course, electromagnetic waves. But, more of this later. We are now in a position to write out Maxwell's equations in all their glory! We get
 (1.15a)
(1.15a)
 (1.15b)
(1.15b)
 (1.15c)
(1.15c)
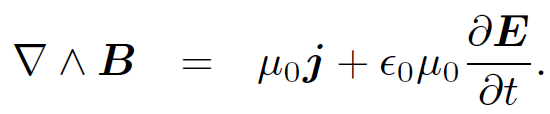 (1.15d)
(1.15d)
These four partial differential equations constitute a complete description of the behaviour of electric and magnetic fields. The first equation describes how electric fields are induced by charges. The second equation says that there is no such thing as a magnetic charge. The third equation describes the induction of electric fields by changing magnetic fields, and the fourth equation describes the generation of magnetic fields by electric currents and the induction of magnetic fields by changing electric fields. Note that with the inclusion of the displacement current these equations treat electric and magnetic fields on an equal footing; i.e., electric fields can induce magnetic fields, and vice versa. Equations (1.15) sum up the experimental results of Coulomb, Ampere, and Faraday very succinctly; they are called Maxwell's equations because James Clerk Maxwell was the first to write them down (in component form). Maxwell also fixed them up so that they made mathematical sense.
 الاكثر قراءة في الكهرومغناطيسية
الاكثر قراءة في الكهرومغناطيسية
 اخر الاخبار
اخر الاخبار
اخبار العتبة العباسية المقدسة

الآخبار الصحية















 قسم الشؤون الفكرية يصدر كتاباً يوثق تاريخ السدانة في العتبة العباسية المقدسة
قسم الشؤون الفكرية يصدر كتاباً يوثق تاريخ السدانة في العتبة العباسية المقدسة "المهمة".. إصدار قصصي يوثّق القصص الفائزة في مسابقة فتوى الدفاع المقدسة للقصة القصيرة
"المهمة".. إصدار قصصي يوثّق القصص الفائزة في مسابقة فتوى الدفاع المقدسة للقصة القصيرة (نوافذ).. إصدار أدبي يوثق القصص الفائزة في مسابقة الإمام العسكري (عليه السلام)
(نوافذ).. إصدار أدبي يوثق القصص الفائزة في مسابقة الإمام العسكري (عليه السلام)


















