
تاريخ الفيزياء

علماء الفيزياء


الفيزياء الكلاسيكية

الميكانيك

الديناميكا الحرارية


الكهربائية والمغناطيسية

الكهربائية

المغناطيسية

الكهرومغناطيسية


علم البصريات

تاريخ علم البصريات

الضوء

مواضيع عامة في علم البصريات

الصوت


الفيزياء الحديثة


النظرية النسبية

النظرية النسبية الخاصة

النظرية النسبية العامة

مواضيع عامة في النظرية النسبية

ميكانيكا الكم

الفيزياء الذرية

الفيزياء الجزيئية


الفيزياء النووية

مواضيع عامة في الفيزياء النووية

النشاط الاشعاعي


فيزياء الحالة الصلبة

الموصلات

أشباه الموصلات

العوازل

مواضيع عامة في الفيزياء الصلبة

فيزياء الجوامد


الليزر

أنواع الليزر

بعض تطبيقات الليزر

مواضيع عامة في الليزر


علم الفلك

تاريخ وعلماء علم الفلك

الثقوب السوداء


المجموعة الشمسية

الشمس

كوكب عطارد

كوكب الزهرة

كوكب الأرض

كوكب المريخ

كوكب المشتري

كوكب زحل

كوكب أورانوس

كوكب نبتون

كوكب بلوتو

القمر

كواكب ومواضيع اخرى

مواضيع عامة في علم الفلك

النجوم

البلازما

الألكترونيات

خواص المادة


الطاقة البديلة

الطاقة الشمسية

مواضيع عامة في الطاقة البديلة

المد والجزر

فيزياء الجسيمات


الفيزياء والعلوم الأخرى

الفيزياء الكيميائية

الفيزياء الرياضية

الفيزياء الحيوية

الفيزياء العامة


مواضيع عامة في الفيزياء

تجارب فيزيائية

مصطلحات وتعاريف فيزيائية

وحدات القياس الفيزيائية

طرائف الفيزياء

مواضيع اخرى
Radiation
المؤلف:
Richard Feynman, Robert Leighton and Matthew Sands
المصدر:
The Feynman Lectures on Physics
الجزء والصفحة:
Volume I, Chapter 28
2024-03-18
2050
Now let us use it to discuss the phenomena called radiation. To discuss these phenomena, we must select from Eq. (28.3) only that piece which varies inversely as the distance and not as the square of the distance. It turns out that when we finally do find that piece, it is so simple in its form that it is legitimate to study optics and electrodynamics in an elementary way by taking it as “the law” of the electric field produced by a moving charge far away. We shall take it temporarily as a given law which we will learn about in detail next year.
Of the terms appearing in (28.3), the first one evidently goes inversely as the square of the distance, and the second is only a correction for delay, so it is easy to show that both of them vary inversely as the square of the distance. All of the effects we are interested in come from the third term, which is not very complicated, after all. What this term says is: look at the charge and note the direction of the unit vector (we can project the end of it onto the surface of a unit sphere). As the charge moves around, the unit vector wiggles, and the acceleration of that unit vector is what we are looking for. That is all. Thus
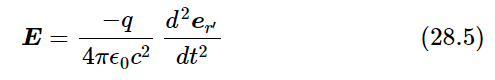
is a statement of the laws of radiation, because that is the only important term when we get far enough away that the fields are varying inversely as the distance. (The parts that go as the square have fallen off so much that we are not interested in them.)
Now we can go a little bit further in studying (28.5) to see what it means. Suppose a charge is moving in any manner whatsoever, and we are observing it from a distance. We imagine for a moment that in a sense it is “lit up” (although it is light that we are trying to explain); we imagine it as a little white dot. Then we would see this white dot running around. But we don’t see exactly how it is running around right now, because of the delay that we have been talking about. What counts is how it was moving earlier. The unit vector er′ is pointed toward the apparent position of the charge. Of course, the end of er′ goes on a slight curve, so that its acceleration has two components. One is the transverse piece, because the end of it goes up and down, and the other is a radial piece because it stays on a sphere. It is easy to demonstrate that the latter is much smaller and varies as the inverse square of r when r is very great. This is easy to see, for when we imagine that we move a given source farther and farther away, then the wigglings of er′ look smaller and smaller, inversely as the distance, but the radial component of acceleration is varying much more rapidly than inversely as the distance. So for practical purposes all we have to do is project the motion on a plane at unit distance. Therefore we find the following rule: Imagine that we look at the moving charge and that everything we see is delayed—like a painter trying to paint a scene on a screen at a unit distance. A real painter, of course, does not take into account the fact that light is going at a certain speed, but paints the world as he sees it. We want to see what his picture would look like. So we see a dot, representing the charge, moving about in the picture. The acceleration of that dot is proportional to the electric field. That is all—all we need.
Thus Eq. (28.5) is the complete and correct formula for radiation; even relativity effects are all contained in it. However, we often want to apply it to a still simpler circumstance in which the charges are moving only a small distance at a relatively slow rate. Since they are moving slowly, they do not move an appreciable distance from where they start, so that the delay time is practically constant. Then the law is still simpler, because the delay time is fixed. Thus we imagine that the charge is executing a very tiny motion at an effectively constant distance. The delay at the distance r is r/c. Then our rule becomes the following: If the charged object is moving in a very small motion and it is laterally displaced by the distance x(t), then the angle that the unit vector er′ is displaced is x/r, and since r is practically constant, the x-component of d2er′/dt2 is simply the acceleration of x itself at an earlier time divided by r, and so finally we get the law we want, which is
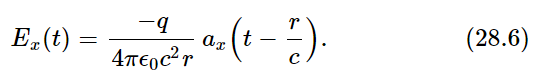
Only the component ax, perpendicular to the line of sight, is important. Let us see why that is. Evidently, if the charge is moving in and out straight at us, the unit vector in that direction does not wiggle at all, and it has no acceleration. So it is only the sidewise motion which is important, only the acceleration that we see projected on the screen.
 الاكثر قراءة في الكهرومغناطيسية
الاكثر قراءة في الكهرومغناطيسية
 اخر الاخبار
اخر الاخبار
اخبار العتبة العباسية المقدسة

الآخبار الصحية















 قسم الشؤون الفكرية يصدر كتاباً يوثق تاريخ السدانة في العتبة العباسية المقدسة
قسم الشؤون الفكرية يصدر كتاباً يوثق تاريخ السدانة في العتبة العباسية المقدسة "المهمة".. إصدار قصصي يوثّق القصص الفائزة في مسابقة فتوى الدفاع المقدسة للقصة القصيرة
"المهمة".. إصدار قصصي يوثّق القصص الفائزة في مسابقة فتوى الدفاع المقدسة للقصة القصيرة (نوافذ).. إصدار أدبي يوثق القصص الفائزة في مسابقة الإمام العسكري (عليه السلام)
(نوافذ).. إصدار أدبي يوثق القصص الفائزة في مسابقة الإمام العسكري (عليه السلام)


















