Two important approximations: The rotating wave approximation and the slowly varying amplitude approximation

We first treat the rotating wave approximation. To this end we decompose the mode amplitudes E_λ (t) into their positive and negative frequency parts

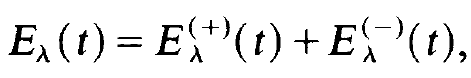     (1.1)

where these parts are defined by

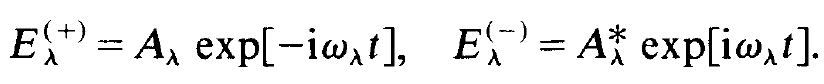    (1.2)

We shall admit that the amplitudes A_λ and A_λ^* are time dependent, but that their time dependence is much slower than that of the exponential functions in (1.2). We further recall that according to, a, contains a rapidly oscillating factor

    (1.3)

Let us now consider typical expressions occurring on the r.h.s.

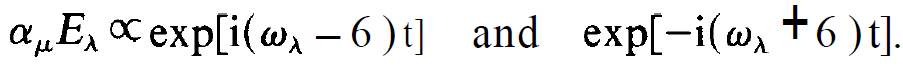 (1.4)

As it will turn out by means of our later calculations, for the laser process only such mode frequencies ⍵_λ are important which lie close to the atomic transition frequency . The exponential functions occurring in (1.4) are quite different, because in one of them the difference of ⍵_λ and 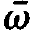 occurs, whereas in the other one the sum .of  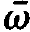and ⍵_λ is present. When we integrate over a time interval which is long compared to the time of a single oscillation t₀= 2π/ 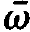but small compared with times over which 'the amplitudes A_λ and A_λ^* vary, the following happens. The exponential function occurring in (1.4) which contains the sum of the frequencies, ⍵_λ +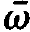, oscillates very rapidly so that when integrated over a time t₀ this contribution vanishes. On the other hand, during that time the exponential function in (1.4) which depends on the frequency difference has not changed appreciably. As a consequence we may ignore the second term occurring in (1.4) against the first term. Transforms into

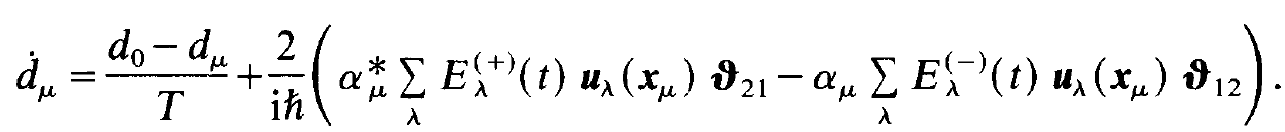    (1.5)

To this end we recall that a, contains the rapidly. When we multiply the equation for a, on both sides by exp[-i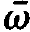 t] it hits quantities E_λ thus producing terms of the form (1.4). This allows us to apply the rotating wave approximation, too. We thus obtain

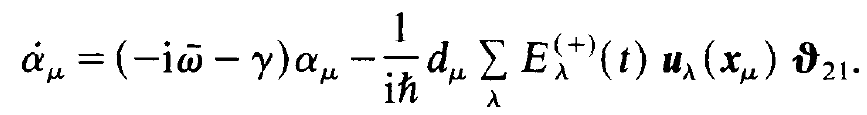   (1.6)

Eventually we may decompose the quantities E_λ and P_λ occurring into their positive and negative frequency parts. We thus obtain the field equation

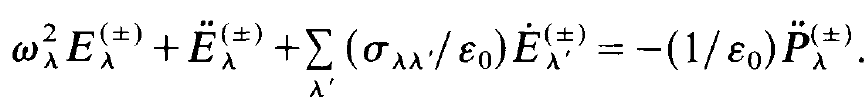    (1.7)

Eqs. (1.5) to (1.7) again represent a closed set of field and matter equations. Our next task will be to further simplify eq. (1.7). This can be achieved by the slowly varying amplitude approximation. To this end we consider for example the positive frequency part E_λ⁽⁺⁾

 (1.8)

As we shall see in later chapters, in general it will not be allowed to assume that the amplitudes A_λ are time independent. But it will turn out that A_λ will change much more slowly than its accompanying exponential function. This may be visualized by saying that A_λ performs much fewer oscillations per unit time than its accompanying exponential function. Therefore we may assume that the temporal derivative of A_λ is much smaller than ⍵_λA_λ, i.e.

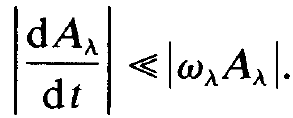   (1.9)

We use this inequality as follows. Differentiating (1.8) on both sides with respect to time we obtain

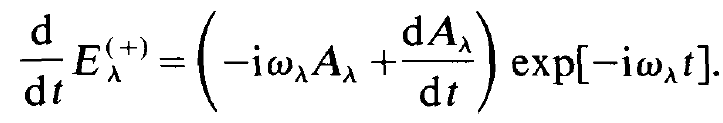    (1.10)

But according to (1.9) we may replace (1.10) by

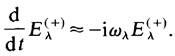    (1.11)

In a similar way we proceed with respect to the second derivatives and

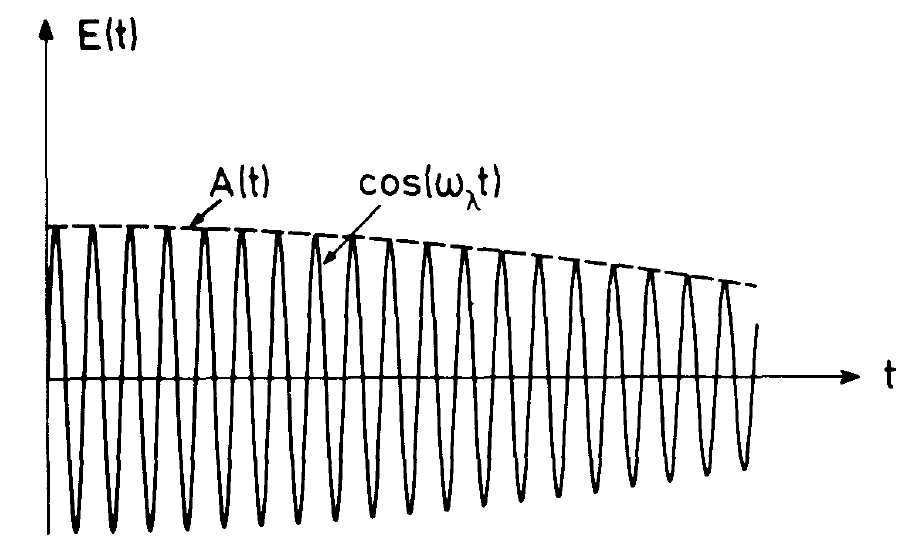
Fig. 1.1. The electric field strength E(t) consists of an envelope A(t) and a cosine function.

consider the expression

 (1.12)

Using the decomposition (1.8) we obtain the following expression for (1.12)

 (1.13)

In analogy to (1.9) we assume that also the inequality

 (1.14)

holds. Within this approximation the leading term of (1.13) is obtained as follows:

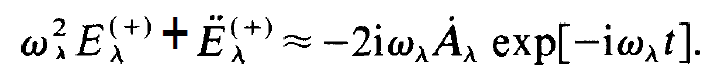 (1.15)

In the following we are primarily interested in E_λ instead of A_λ. Therefore we express A_λ by E_λ whereby (1.15) is transformed into

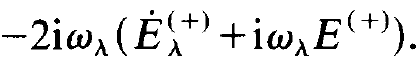 (1.16)

In a similar way we may proceed with the polarization P_λ. Because there is no need to repeat all arguments once again we immediately write down the result

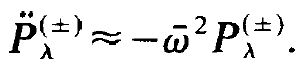 (1.17)

For sake of simplicity we shall assume in the following that

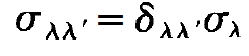 (1.18)

holds, i.e. only those contributions of σ_λλʹ are assumed different from 0 for which A = λʹ. Using the approximations (1.11), (1.16) and (1.17) we may transform the original equation for the electric field strength (1.7) into

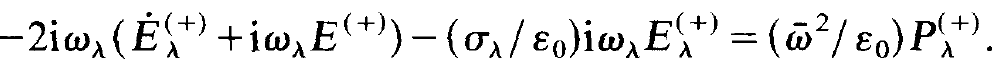   (1.19)

We divide this equation by -2i⍵_λ, introduce the abbreviation

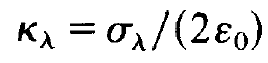 (1.20)

and put all terms except E_λ⁽⁺⁾ on the r.h.s. Thus we eventually obtain the rather simple equation

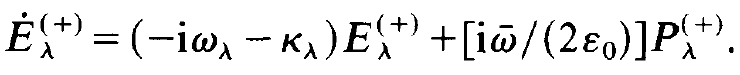    (1.21)

We have assumed in addition that we may replace ⍵_λ by 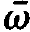 in the last term. Let us summarize the results of this section. We have first introduced the rotating wave approximation and then the slowly varying amplitude approximation. The resulting equations are represented in (1.5), (1.6) and (1.21). These equations may serve as a starting point for the laser theory and they are indeed quite often used in that form. On the other hand it has turned out that these equations can be cast in a still simpler and more symmetric form.