Clausius–Clapeyron

a) Derive the Clausius–Clapeyron equation for the equilibrium of two phases of a substance. Consider a liquid or solid phase in equilibrium with its vapor.

b) Using part (a) and the ideal gas law for the vapor phase, show that the vapor pressure follows the equation ln P_V = A – B/τ. Make reasonable assumptions as required. What is B?

SOLUTION

a) We know that, at equilibrium, the chemical potentials of two phases should be equal:

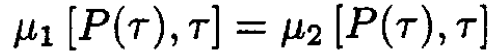(1)

Here we write P ≡ P(τ) to emphasize the fact that the pressure depends on the temperature. By taking the derivative of (1) with respect to temperature, we obtain

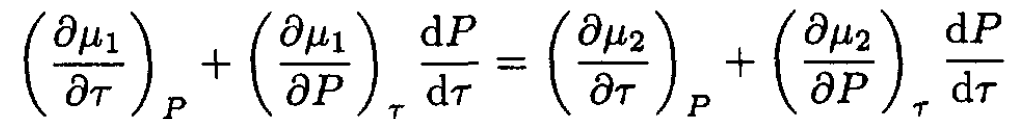(2)

Taking into account that (∂μ/∂τ)_p = -s and (∂μ/∂P)_τ = v, where s and v are the entropy and volume per particle, and substituting into (2), we have

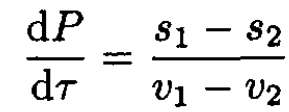(3)

where subscripts 1 and 2 refer to the two phases. On the other hand, q = τ(s₂ – s₁),  where q is the latent heat per particle, so we can rewrite (3) in the form

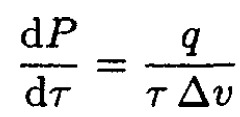(4)

which is the Clausius–Clapeyron equation.

b) Consider the particular case of equilibrium between liquid and vapor. The volume v₁ of the liquid is usually much smaller than that for the vapor v₂, so we can disregard v₁ in (4) and write

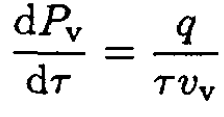(5)

Using the ideal gas law for vapor, v_v = τ/P_v, we get

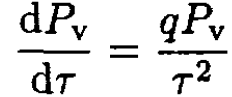(5)

or

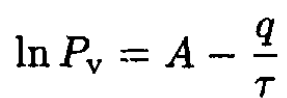(6)

We can see that B = q. Rewriting (6) in usual units gives

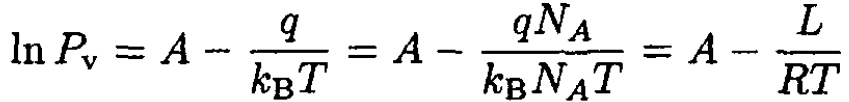
where L is the latent heat per mole, N_A is Avogadro’s number, and R is the gas constant.