Bose Condensation Critical Parameters

Consider an ideal Bose gas of N particles of mass m and spin zero in a volume V and temperature τ above the condensation point.

a) What is the critical volume V_C below which Bose–Einstein condensation occurs? An answer up to a numerical constant will be sufficient.

b) What is the answer to (a) in two dimensions?

SOLUTION

a) The number of particles dN in an element of phase space is given by

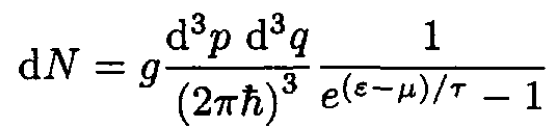(1)

where g = 2S + 1. With the usual dispersion law for an ideal gas ε = p²/2m and integrating over d³q, we find the particle distribution over energy:

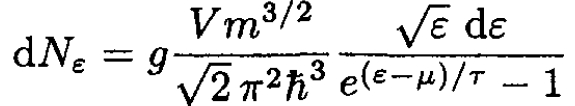(2)

Integrating (2), we obtain a formula for the total number N of particles in the gas:

(3)

Letting ε/τ = x, we rewrite (3) as

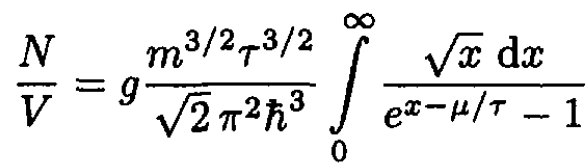(4)

(4) defines a parametric equation for the chemical potential μ. The decrease of volume (or temperature) will increase the value of the integral, and therefore the value of μ (which is always negative in Bose statistics) will increase. The critical parameters V_c or τ_c correspond to the point where μ = 0 (i.e., if you decrease the volume or temperature any further, μ should increase even further to provide a solution to (4), whereas it cannot become positive). So we can write at a certain temperature:

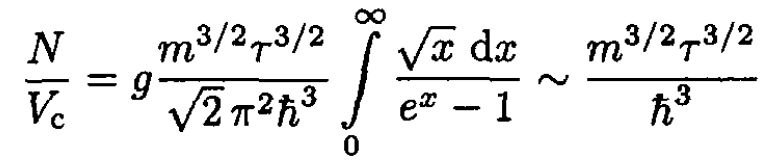(5)

Therefore,

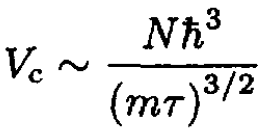(6)

b) In two dimensions the integral (3) becomes

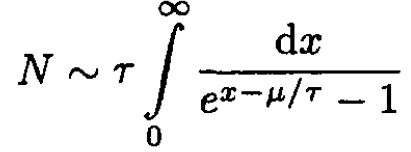
and there is no Bose condensation.